Rechnen in (bzw. 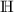) — Teil 2

F: Du hast gesagt, bei einem hyperreellen Term braucht man nur zu untersuchen, ob er eine infinite, eine infinitesimale oder eine sonstige finite Zahl beschreibt. Warum genügt dieses pauschale Rechnen?
A: Wir treiben Analysis mit reellen Funktionen. Für unsere Untersuchungen sind die hyperreellen Zahlen nur Hilfsmittel. Allein mit reellen Zahlen würde der Fehler, den man zum Beispiel beim Berechnen einer Steigung macht, nicht klein genug. Er muss nämlich infinitesimal sein, damit man ihn als unbeachtlich weglassen kann. Das ganze Verfahren besteht darin, die gegebene reelle Funktion zunächst ins Hyperreelle zu erweitern und dort die Rechnung durchzuführen. Stellt sich dann heraus, dass das Ergebnis eine finite Zahl ist, braucht man nur noch ihren reellen Teil zu nehmen. Damit geht man in die reelle Zahlenwelt zurück und erhält somit das gesuchte Ergebnis, zum Beispiel eine Steigung.
F: Das erspart einem das Rechnen mit Zahlenfolgen.
A: Natürlich gibt es Terme, bei denen man Genaueres über die beteiligten Zahlen kennen muss, aber auch dann braucht man normalerweise keine Folgendarstellung.
F: Aus dem ersten Teil unseres Gesprächs habe ich schon erkannt, dass die Summe aus einer infiniten und einer reellen Zahl immer infinit ist. Genauso ist es bei der Addition einer infinitesimalen zu einer infiniten Zahl. Also ist die Summe aus infiniter und finiter Zahl immer infinit.
A: Das ist richtig. Aber wenn zwei infinite Zahlen addiert werden, muss die Summe keineswegs infinit sein.
F: Wieso?
A: Ganz einfach! Addiert man Ω zu Ω hinzu, lautet das Ergebnis 2Ω, welches unverkennbar infinit ist. Aber die Summe aus Ω und −Ω ist gleich null, also reell, sogar infinitesimal. So kannst Du Dir auch Beispiele überlegen, dass die Summe zweier infiniter Zahlen 7 lautet.
F: Nun ja, wenn ich Ω zu −Ω+7 addiere, kommt 7 heraus, also etwas Reelles. Ω + (−Ω) ist gleich null, also infinitesimal. Beim Addieren infiniter Zahlen kann also die Summe von jedem Zahltyp sein.
A: So ist es. Schau Dir doch bitte die folgende Additionstabelle an. Die Zahlen in der linken Spalte und die in der obersten Zeile werden addiert und die Summe steht in der Tabelle im Schnittpunkt der jeweiligen Zeile und Spalte, in denen die Summanden stehen. Für die beteiligten Summanden stehen nur Variable, aber an den verschiedenen Buchstabenarten kannst Du erkennen, für welchen Zahltyp diese Variablen jeweils stehen.

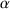• und β, also kleine griechische Buchstaben, für infinitesimale Zahlen,
• x und y vom Ende des lateinischen Alphabets für reelle Zahlen,
• f und g, also aus einem anderen Teil des Alphabets fortlaufend, für finite, aber nicht reelle und nicht infinitesimale Zahlen,
• Γ und Δ, also griechische Großbuchstaben, für infinite Zahlen.

Von einigen Summen hast Du bereits gesagt, welchem Zahltyp sie angehören müssen. Dies habe ich bereits eingetragen. Dort, wo man Genaueres über die beteiligten Summanden wissen muss, um den Zahltyp des Ergebnisses zu kennen, steht ein Fragezeichen. Wenn Du über den Zahltyp des Ergebnisses sicher bist, dann trage den entsprechenden Buchstabentyp ein, also zum Beispiel

• γ, wenn die Summe ganz sicher infinitesimal ist,
• z, wenn die Summe ganz sicher reell ist,
• h, wenn die Summe ganz sicher finit ist, aber nicht unbedingt reell oder infinitesimal,
• Λ, wenn die Summe ganz sicher infinit ist und
• ein Fragezeichen, wenn die Summe finit, infinitesimal oder infinit sein kann, man also Genaueres über die Summanden wissen muss.

Du sollst also nur pauschal den Zahltyp angeben, zu dem eine Summe mit Sicherheit gehört.

( + )	β	y	g	Δ
α	γ	h	h	Λ
x	h	z	h	Λ
f	h	h	h	Λ
Γ	Λ	Λ	Λ	?

F: So würde ich die Tabelle ausfüllen. Dabei habe ich zum Beispiel bei der Summe zweier finiter Zahlen außer Acht gelassen, dass ihre Summe in besonderen Fällen reell oder infinitesimal sein kann. Keinesfalls kann die Summe finiter Zahlen aber infinit sein.
A: Richtig! Es dürfte Dir auch nicht schwerfallen, eine entsprechende Subtraktionstabelle auszufüllen. Wir verwenden die Symbole wieder in gleicher Weise. Rechne in der Tabelle immer linke Zahl minus obere Zahl, damit es keine Verwechslungen gibt, denn Du weißt ja, dass die Subtraktion nicht kommutativ ist.

( − )	β	y	g	Δ
α	γ	h	h	Λ
x	h	z	h	Λ
f	h	h	h	Λ
Γ	Λ	Λ	Λ	?

F: Diese Aufgabe war leicht, denn ich brauchte nur daran zu denken, dass eine Subtraktion gleichbedeutend mit der Addition der Gegenzahl ist. Weil sich dabei an den Größenordnungen der Zahlen nichts ändert, sieht folglich die Subtraktionstabelle genauso aus wie die Additionstabelle.
A: Richtig, so einfach ist das also. Dann überlege Dir nun, was in der Multiplikationstabelle stehen muss.

( × )	β	y	g	Δ
α	γ	γ	γ	?
x	γ	z	h	Λ
f	γ	h	h	?
Γ	?	Λ	?	Λ

F: Auch in diese Tabelle habe ich immer die allgemeinen Fälle eingetragen. Zwar kann zum Beispiel das Produkt Γ × g auch infinitesimal sein, nämlich wenn g gleich 0 ist, aber solche Sonderfälle soll ich ja außer acht lassen.
A: Ja, da hast Du aufgepasst. Aber trotzdem enthält die Tabelle Fragezeichen, die Du noch begründen musst.
F: Dazu brauche ich Dir nur Beispiele zu nennen. Nehmen wir einmal die hypernatürliche Zahl = (1; 2; 3; 4; 5; ...) und ihre Kehrzahl = (1; 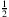; ; 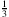; ; 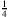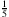...), dann ist ganz bestimmt

• ω × = 1, also finit, sogar reell,
• ω² × = ω × 1 = ω, also infinitesimal, und
• ω × ² = 1 × = , also infinit.

Da die Multiplikation kommutativ ist, ich also die Faktoren immer vertauschen kann, sind damit sogar beide Fragezeichen erklärt.
A: Gut! Nun fehlt nur noch die Divisionstabelle.

( : )	β≠0	y≠0	g≠0	Δ
α
x
f
Γ

Lösung: