Die hyperreelle Zahlengerade

F: Ist es möglich, hyperreelle Zahlen, insbesondere die infinitesimalen und die infiniten, auf der Zahlengeraden darzustellen?
A: Das ist allein schon deshalb möglich, weil man hyperreelle Zahlen, genauso wie die reellen, anordnen kann. Anordnen heißt ja, dass man von zwei Zahlen immer sagen kann, welche die größere ist oder ob sie gleich sind. Es treten aber ein paar Besonderheiten auf, weil es in der Zahlenmenge 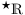(bzw. 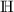) auch Zahlen mit unendlich großem und unendlich kleinem Betrag gibt.
F: Das hängt doch bestimmt mit dem Maßstab zusammen, den ich für die Zahlengerade wählen muss.
A: So ist es, denn bekanntlich wählt man für das, was man darstellen will, immer einen dafür geeigneten Maßstab. Deshalb wollen wir mit einer kleinen Vorübung beginnen. Das folgende Bild zeigt die reelle Zahlengerade so, wie Du sie kennst, in drei verschiedenen Maßstäben. Erkennst Du, wie man von einer Zeichnung in die andere umrechnet?



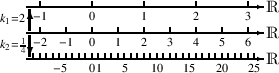
F: Man sieht es schon. Die Nullen aller drei Geraden stehen übereinander, die obere Zahlengerade ist gegenüber der mittleren um den Faktor zwei vergrößert, die untere dagegen entsteht, wenn man auf die mittlere den Faktor 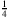anwendet.
A: Jetzt muss man aufpassen, dass man die Worte eindeutig verwendet. Eigentlich ist die untere Zahlengerade verkleinert gegenüber der mittleren, jedoch muss man sagen, sie ist "um den Faktor 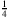vergrößert"...
F: ... oder "um den Faktor 4 verkleinert". Aber ist es nicht Unsinn, von Vergrößerung oder Verkleinerung der Zahlengeraden zu sprechen, wenn die doch sowieso unendlich lang ist?
A: Da hast Du selbstverständlich recht. Es ist nämlich besser, anzugeben, wieviel Einheiten eine vorgegebene Vergleichsstrecke im gewählten Maßstab besitzt. Diese Vergleichsstrecke soll auf allen Zahlengeraden, unabhängig von ihrem Maßstab, immer gleich lang sein. Denk an ein kariertes Zeichenblatt, dessen Linien einen festen Abstand voneinander besitzen. Das erkennst Du im folgenden Bild. Ich habe die hyperreelle Zahlengerade übrigens nicht mit 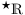bezeichnet, sondern mit 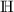, weil ich das einprägsamer finde.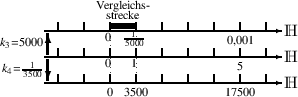



F: Stimmt, die Strecke, die in der mittleren Zahlengeraden die Länge 1 hat, hat in der oberen die Länge 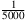und in der unteren die Länge 3500. Und die Umrechnungsfaktoren 5000 und 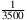stehen auch dabei.
A: Die feste Vergleichsstrecke, die in der Mitte das Maß m_alt = 1 hatte, hat oben das Maß m_neu = 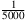, weil auf die Zahlengerade der Faktor k = 5000 angewendet wurde. Zwischen m_neu und m_alt gilt also der Zusammenhang m_neu = m_alt⁄k.
F: Das bedeutet doch, dass k infinit sein muss, damit die Vergleichsstrecke ein infinitesimales Maß bekommt.
A: So ist es. Aber damit man diesen Faktor anwenden kann, muss man aus der reellen Zahlengeraden eine hyperreelle machen, die zusätzlichen Zahlen also hinzufügen. Was meinst Du, wie die hyperreelle Zahlengerade aussieht?
F: Hmm..! Eigentlich genauso wie die reelle oder nicht?
A: Jawohl, nämlich eine durchgezogene Linie. Übrigens ist auch die rationale Zahlengerade eine durchgezogene Linie, denn schon die Zahlenmenge 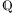ist dicht.
F: Was bedeutet „dicht”?
A: Eine Zahlenmenge nennt man „dicht”, wenn man bei zwei gegebenen Zahlen immer eine dritte angeben kann, die zwischen beiden liegt. Das kann man 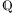bei , bei 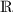und auch bei 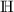(bzw. 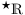) immer machen. Es bleibt gar nichts anderes übrig, als in allen Fällen eine durchgezogene Linie zu zeichnen. Für welche Menge eine Zahlengerade jeweils steht, kann man nur an ihrer Bezeichnung erkennen. Im zweiten Bild über Maßstabsänderungen habe ich, wie Du gesehen hast, das 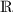durch ein 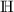ersetzt. Die Bilder der Geraden haben sich dadurch nicht verändert, jedoch verbinden wir eine andere Vorstellung mit den Geraden.
Aber zurück zu Deiner richtigen Vermutung, man müsse einen infiniten Faktor k anwenden, damit die Vergleichsstrecke ein endliches Maß bekommt. Diese infinite Vergrößerung ist etwas Neues, weswegen im folgenden Bild eine „Unendlichkeitsbrille” (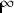) gezeichnet ist. Außerdem findet nun die Vergrößerung nicht bei der Null statt, sondern bei irgendeiner reellen Zahl r. Im folgenden Bild bleibt also die Zahl r am selben Ort. Beschreibe bitte, was Du siehst.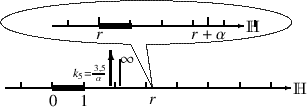



F: Offenbar soll die Zahl 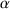infinitesimal sein, dann ist der Vergrößerungsfaktor 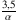tatsächlich infinit. Folglich finde ich die Zahl r+ 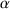jetzt 3,5mal so weit von r entfernt wie die Vergleichsstrecke lang ist.
A: Richtig! Und nun sag bitte, wo Du die Null suchen würdest.
F: Auf jeden Fall links davon. Und wenn ich es richtig sehe, kann ich sie auf keinem noch so großen Zeichenblatt mehr unterbringen, denn sie ist natürlich in dieser Vergrößerung infinit weit weg.
A: Und das gilt nicht nur für die Null. Bei einer infiniten Vergrößerung bleibt nur diejenige reelle Zahl sichtbar, bei der vergrößert wurde. Alle anderen reellen Zahlen sind unendlich weit weggerückt, denn sie alle haben einen Abstand von r, der nicht infinitesimal ist. Somit sind alle nicht infinitesimalen Längen unendlich vergrößert. Deshalb habe ich die vergrößerte Zahlengerade in eine Art Blase hineingezeichnet, denn sie enthält nur eine einzige reelle Zahl mit ihrer infinitesimalen Umgebung.
F: Damit habe ich zunächst nicht gerechnet, aber was Du sagst, stimmt. Das sehe ich jetzt auch. Das bedeutet doch, dass ich, um infinitesimale Zahlen darzustellen, bei null die Unendlichkeitsbrille anwenden muss, dass dann aber keine reelle Zahl, außer null natürlich, sichtbar sein kann, da sie ja alle im Infiniten gezeichnet werden müssten, so wie hier.



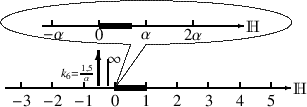
A: Völlig richtig! Aber das ist noch nicht alles. Da man mit infinitesimalen Zahlen rechnen kann, gibt es natürlich auch die Zahl 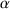². Wie würdest Du denn 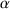² sichtbar machen?
F: Hm..! Bei 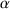² wird ja das infinitesimale 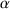noch einmal mit etwas Infinitesimalem multipliziert. Dann ist also 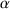² infinitesimal benachbart zu 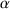, kann also in meiner Zeichnung noch gar nicht erkennbar sein. Dann muss ich doch bei 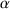noch ein weiteres Mal die Unendlichkeitsbrille anwenden. Ist das richtig?
A: Na klar! Und wo ist dann zum Beispiel 2 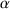zu suchen?
F: In dieser doppelt infiniten Vergrößerung ist es infinit weit weg.
A: Richtig! Du siehst also, dass es verschiedene Größenordnungen von Infinitesimalität gibt. Das muss man übrigens bedenken, wenn man bei hyperreellen Termen beurteilen will, ob sie finite, infinite oder infinitesimale Zahlen beschreiben. Mit sichtbarem 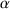² sieht Deine ergänzte Zeichnung also folgendermaßen aus.



Ich glaube, nun fällt es Dir nicht schwer, zu sagen, wie man infinite Zahlen auf der Zahlengeraden sichtbar macht.
F: Ich will bei unserer Sprechweise bleiben. Die Vergleichsstrecke muss ein infinites Maß bekommen, also ist entsprechend m_neu = m_alt⁄k ein infinitesimaler Faktor k anzuwenden. Dann sind rechts von null nur positv infinite Zahlen und links von ihr nur negativ infinite zeichenbar.
A: Und was ist mit den finiten Zahlen, zum Beispiel der reellen 1000?
F: Die 1000 wäre so dicht an der Null zu zeichnen, dass sie in diesem Maßstab ... Sind dann nicht alle finiten Zahlen infinitesimal nahe an der Null zu zeichnen?
A: Richtig, darum kann man getrost am Übergang von den negativ infiniten zu den positiv infiniten Zahlen ein statt einer Null hinschreiben, denn der gesamte reelle Zahlenkörper ist, in dieser Vergrößerung wohlgemerkt, so stark zusammengeschrumpft. Zu zeichnen wäre das wie hier. Beachte die Richtung des Pfeils neben der Unendlichkeitsbrille, denn auch in diesem Falle ist in der Blase der Ausschnitt zu denken. Auf der unteren Zahlengeraden ist die infinite Zahl sichtbar, alle finiten Zahlen befnden sich „in der Mitte”, infinitesimal zusammengeschrumpft.



F: Dort befinden sich natürlich auch die „echt” infintesimalen Zahlen. Die hyperreelle Zahlengerade hat wirklich eine eigenartige Struktur.
A: Ja, da hast Du durchaus recht. Aber als kleine Übung solltest Du Dir überlegen, wie man denn die Zahl 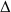² sichtbar macht.
F: Das entspricht gedanklich dem, wie man ein infinitesimales 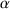² sichtbar macht. Um 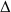² sichtbar zu machen, ist erneut ein infinititer Faktor k anzuwenden. Alle „einfach” infiniten Zahlen wie sind in der infinitesimalen Umgebung von null zu denken, so wie hier.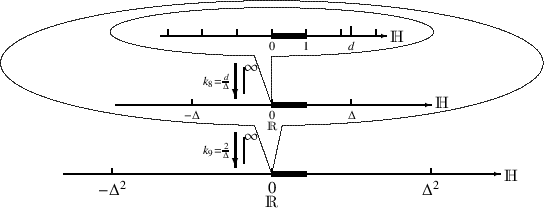



Gibt es denn keine Möglichkeit, alle hyperreellen Zahlentypen, also infinite und finite, in einem Bild zu zeichnen, ohne dass die einen zu einem Punkt zusammenschrumpfen oder unendlich weit weg sind?
A: Das geht nur, wenn man auf einen festen Maßstab verzichtet. Das dürfte Dir aus unseren bisherigen Überlegungen klargeworden sein. Solch eine „lange” Zahlengerade könnte man dann folgendermaßen zeichnen.



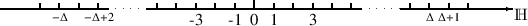
F: Warum zeichnest Du sie nicht mehr durch? Ist die Menge 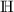(bzw. 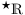) plötzlich nicht mehr „dicht”?
A: Doch, die Menge 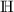(bzw. 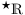) ist sehr wohl überall dicht. Die Punktierungen sind notwendig, weil der Übergang vom Finiten ins Infinite nicht angegeben werden kann.
F: Das musst Du mir bitte noch erklären.
A: Das ist leicht zu beweisen. Du kannst nämlich nicht die letzte finite Zahl angeben. Denn würdest Du mir eine nennen und als die größte „verkaufen” wollen, dann sage ich Dir sofort eine noch größere, zum Beispiel Deine Zahl plus eins, und die wäre ebenfalls finit. Es ist also keine größte finite Zahl angebbar.
F: Ach so, na klar! Und würde ich Dir eine infinite Zahl als kleinste ihrer Art „verkaufen” wollen, dann sagst Du mir sofort eine zum Beispiel um fünf kleinere, und die wäre ebenfalls infinit. Also kann man den Übergang von finit nach infinit wirklich nicht angeben, weswegen man die Zahlengerade dort punkktieren muss.
Entsprechendes gilt dann aber auch für den Übergang infinitesimal – finit oder nicht?
A: Ja, so ist es. Du hast Dich vorhin schon über die eigenartige Struktur der Menge 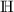(bzw. 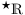) gewundert. Man muss sie sich wirklich so vorstellen, als wäre jede Zahl von einer Wolke von Zahlen kleinerer Größenordnungen umgeben. Aber das ist immer noch nicht alles. Wo würdest Du denn bei der unmaßstäblichen „langen” Zahlengeraden die Zahl 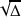suchen?
F: Oh, das ist gar nicht so einfach. 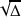kann nicht finit sein, denn mit sich selbst multipliziert muss sich das infinite 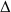ergeben. Also ist 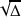infinit. Aber sie kann nicht in demselben Teil der Zahlengeraden sein wie .
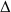A: Richtig! Es gibt also auch in unserem gestrichelten Teil wieder Bereiche , die man bei passender Vergrößerung durchzeichnen kann. Die Menge 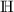(bzw. 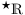) sorgt doch immer wieder für Überraschungen, nicht wahr?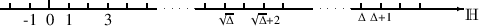



Und wo würdest Du auf der „langen” Zahlengerade 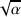suchen? Wie würdest Du zeichnen?
F: Auch 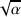würde wieder in einem eigenen Bereich liegen, den ich mit Strichelungen von dem Bereich mit 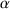trennen muss. Weil aber infinitesimale Zahlen betragsmäßig zwischen null und eins liegen, ist größer als 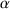, liegt also rechts davon.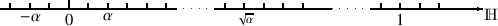



A: Genau! Richtig ist auch, dass die Eins in einem Bereich der „langen” Zahlengeraden liegt, der von 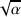mit Punktierungen zu trennen ist.
Und nun habe ich noch eine letzte Aufgabe für Dich.
Die bisher gezeichneten „langen” Zahlengeraden besitzen in allen Teilen jeweils denselben Maßstab. Schau Dir zum Beispiel an, an welchen Markierungen die Bezeichnungen − 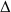und −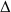+2 stehen, wenn Du sie mit 1 und 3 vergleichst. Schreib doch auch im letzten Bild an einige Markierungen, welche Zahlen dort liegen.