Wie man den reellen Zahlenkörper erweitert

F: Kann es denn zusätzlich zu den reellen Zahlen überhaupt noch weitere Zahlen geben? Immerhin heißt es doch, die Menge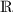 sei vollständig.
A: Wieso soll es denn keine zusätzlichen Zahlen geben? Ich könnte Dir gleich mehrere Beispiele nennen, bei denen man zu vorhandenen Zahlen neue hinzugefügt hat. Denk an die negativen Zahlen, die Bruchzahlen oder daran, wie man die irrationalen Zahlen gefunden hat.
F: Die reellen Zahlen sind zusätzliche Zahlen, die es vorher nicht gab?
A: Ja, sogar die rationalen Zahlen sind schon neue Zahlen gewesen, als man verlangte, dass nicht nur jede Additions- und Multiplikationsaufgabe ein Ergebnis haben sollte, sondern auch jede Subtraktions- und jede Divisionsaufgabe. So erhielt man negative Zahlen und die Brüche als neue Zahlen. Am Anfang stand ja nur das Zählen, wofür bekanntlich die natürlichen Zahlen ausreichen.
F: Und was hat das mit den hyperreellen Zahlen zu tun?
A: Eine ganze Menge, denn wenn man die Grundrechenarten mit rationalen Zahlen durchführt, erhält man wieder nur rationale Zahlen als Ergebnis. Deswegen sagt man auch, die Zahlenmenge 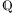sei abgeschlossen. Und dieses Wort lässt einen ebenfalls denken, als gäbe es keine weiteren Zahlen mehr.
F: Ich verstehe. Die Menge 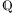ist abgeschlossen bezüglich der Grundrechenarten. Aber warum haben sich die Mathematiker denn nicht damit zufrieden gegeben?
A: Denke zum Beispiel an die Frage, wie man die Länge der Diagonalen in einem Quadrat aus der Länge seiner Seite berechnet. Schon Euklid hat herausgefunden, dass man die Seitenlänge mit einer Zahl multiplizieren muss, die gar nicht rational sein kann. Heute bezeichnen wir diese Zahl mit . Ein anderes Beispiel ist die Zahl 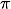, mit der man aus dem Durchmesser eines Kreises seinen Umfang berechnet und die ebenfalls nicht rational ist.
F: Ja, ich erinnere mich an meine Schulzeit, so etwa in der neunten Klasse muss es gewesen sein. Da haben wir untersucht, wo genau auf der Zahlengeraden liegt. Wir konnten nie exakt angeben. So viele Dezimalstellen wir auch hinzufügten, immer waren diese rationalen Zahlen entweder zu klein oder zu groß. lag immer im Intervall zwischen zwei rationalen Zahlen. Diese Intervalle wurden zwar immer kleiner ... . Ja, jetzt weiß ich es wieder, Intervallschachtelung hat das unser Lehrer genannt, weil die kleineren Intervalle immer innerhalb der größeren liegen, genau wie bei der russischen Matrjoschka-Puppe, bei der man in jeder Puppe eine noch kleinere findet, wenn man sie öffnet.
A: Wichtig ist, dass man die Zahl nicht mehr mit den Grundrechenarten findet, sondern mit einem anderen Verfahren, nämlich der Intervallschachtelung. Man legt nämlich fest, dass man genau die gesuchte findet, wenn man immer so fortschreitet, also die Intervalle immer kleiner macht, aber bei jedem Schritt verlangt, dass das neue, kleinere Intervall innerhalb des größeren liegt, eben genau wie bei Matrjoschka.
Du siehst also, dass man aus den rationalen Zahlen mit einem anderen Verfahren durchaus andere, neue Zahlen finden kann. Diese neuen, nicht mehr rationalen, Zahlen nannten Mathematiker irrationale Zahlen.
F: Die rationalen und die irrationalen Zahlen fasst man nun zur Menge 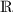der reellen Zahlen zusammen. Jetzt verstehe ich. Neue Zahlen kann man nicht mehr finden, wenn man bei demselben Verfahren bleibt, denn Intervallschachtelungen mit reellen Zahlen ergeben immer wieder nur reelle Zahlen. Wegen dieses Verfahrens also bezeichnet man die Menge 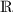als vollständig. Würde man ein anderes Verfahren festlegen, dann kann man durchaus wieder Zahlen finden, die es vorher nicht gab.
A: Du hast das Entscheidende verstanden. Aber Vorsicht, völlig beliebig kann man nicht vorgehen, wenn man neue Zahlen erklären will. Es ist dabei immer zu beachten, dass man mit dem neuen Verfahren nicht nur neue Zahlen findet, sondern auch die alten wiederfinden kann. Umgekehrt müssen die Rechengesetze, die bei den alten Zahlen galten, bei den neuen Zahlen weitergelten. Bei den reellen Zahlen ist es so. Zum einen können Intervallschachtelungen auch auf rationale Zahlen führen, zum andern gelten auch bei irrationalen Zahlen Kommutativ- und Assoziativgesetze sowie das Distributivgesetz. Null und Eins bleiben die neutralen Zahlen bei Addition bzw. Multiplikation, und auch jede irrationale Zahl hat ihre Gegenzahl und ihren Kehrwert, die natürlich beide irrational sein müssen.
F: Alles klar: Die Zahlenmenge 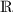mit den Rechengesetzen und den neutralen Zahlen 0 und 1 ist ein Erweiterungskörper von 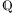. Aber welches Verfahren führt nun aus 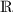hinaus?
A: Das kommt ganz darauf an, was für Zahlen man braucht. Für die Analysis benötigt man Zahlen mit unendlich kleinem und unendlich großem Betrag. Letztere gibt es in 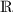überhaupt nicht, und einen unendlich kleinen Betrag hat in 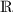nur die Null. Aber die hat den Nachteil, dass man durch sie nicht dividieren kann.
F: Aber die Menge 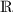reicht doch bis ins Unendliche.
A: Vorsicht! Du bringst hier etwas durcheinander. Es gibt zwar keine größte reelle Zahl, aber jede reelle Zahl, die Du mir nennst, und sei sie noch so groß, wird endlich sein. Ich kann Dir nämlich immer sofort eine noch größere nennen, und Du wieder eine noch größere. Aber alle diese Zahlen werden immer endlich sein. Man nennt deshalb die reellen Zahlen potentiell unendlich. Die Analysis benötigt aber Zahlen, die aktual unendlich sind. Diese müssen also tatsächlich im Unendlichen liegen, jenseits der reellen Zahlen. Nur dann kann man im Unendlichen auch rechnen.
F: Nun sag schon, wie man sie findet!
A: Betrachten wir zunächst noch einmal die Intervallschachtelungen genauer, und zwar ihre Ränder. Bei könnte die Abfolge der linken Ränder beispielsweise so aussehen: Alle diese rationalen Zahlen sind kleiner als . Und ein Beispiel einer Abfolge rechter Ränder für wäre Auch dies sind alles rationale Zahlen, nun aber größer als .
Mathematische Gebilde wie diese beiden Beispiele nennt man Zahlenfolgen. Im ersten Beispiel werden die Zahlen von Folgenglied zu Folgenglied immer größer, die Folge nennt man deshalb monoton wachsend, das zweite Beispiel ist eine monoton fallende Folge, weil ihre Folgenglieder immer kleiner werden. Beide Folgen haben etwas gemeinsam: die Folgenglieder streben der Zahl zu, kommen ihr also beliebig nahe, erreichen sie aber nie. In der mathematischen Fachsprache spricht man von Cauchy-Folgen, sie sind konvergent, d.h. sie haben einen Grenzwert.
Merken musst Du Dir nun Folgendes. Wenn man mit den alten Zahlen, aber einem neuen Verfahren, neue Zahlen definiert, muss man eine Äquivalenzrelation angeben, also die Bedingung, wann man mit dem Verfahren aus verschiedenen alten Zahlen dieselbe neue Zahl findet. Schau Dir noch einmal die beiden Beispielfolgen für an. Die beiden Folgen stimmen in keinem einzigen (rationalen) Folgenglied überein, aber sie haben denselben Grenzwert. Und deswegen beschreiben sie dieselbe reelle Zahl, nämlich .
Also: Reelle Zahlen werden mittels rationaler Cauchy-Folgen beschrieben. Zwei Cauchy-Folgen beschreiben dieselbe reelle Zahl, wenn sie denselben Grenzwert besitzen.
F: Gibt es denn auch eine Äquivalenzrelation bei der Erweiterung zum Zahlenkörper ?
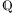A: Ja, selbstverständlich. Die Division zweier natürlicher Zahlen, zum Beispiel 5 : 7, führt auf 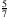. Dividiert man 15 : 21, dann erhält man 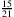. Beide Brüche beschreiben dieselbe rationale Zahl, denn sie gehen mittels Erweitern bzw. Kürzen auseinander hervor. Das ist ja das Schöne an den Bruchzahlen: Man schreibt die Aufgabe nur in einer besonderen Weise hin und sagt, so soll das Ergebnis heißen, das sei also die neue Zahl.
F: Stimmt! Mir fällt auch ein Beispiel für negative Zahlen ein: 5 − 8 hat dasselbe Ergebnis wie 7 − 10 und 12 − 15. Hier ergibt sich die Schreibweise der neuen Zahlen aus der einfachsten denkbaren Aufgabe, die auf die neue Zahl führt, nämlich 0 − 3. Und weil man die Null weglassen kann, erhält man die Schreibweise der neuen Zahl Negativ-Drei, nämlich −3.
A: Und jetzt kommen wir endlich zu den hyperreellen Zahlen und wie man sie herstellt oder findet. Was wir also brauchen, ist

• ein Verfahren, mit dem man sie aus den reellen Zahlen herstellt,
• eine Äquivalenzrelation, aus der hervorgeht, wann das Verfahren mit verschiedenen reellen Zahlen zur selben hyperreellen Zahl führt und
• den Nachweis, dass man die reellen Zahlen in dieser Menge wiederfindet.
• Ferner sind die Rechengesetze für reelle Zahlen auf die größere Zahlenmenge zu übertragen.

Fangen wir mit dem Verfahren an. Jede Folge reeller Zahlen beschreibt eine hyperreelle Zahl. Dienten zur Herstellung reeller Zahlen ausschließlich Cauchy-Folgen, also konvergente Folgen rationaler Zahlen, so sind zur Beschreibung hyperreeller Zahlen zusätzlich auch Folgen wie (1; 2; 3; 4; 5; 6; 7; 8; 9; ...) oder (1; 3; 1; 3; 1; 3; 1; 3; 1; ...} erlaubt, deren Folgenglieder reelle Zahlen sind. Beide Folgen sind divergent, denn sie besitzen keinen Grenzwert. Das erste Folgenbeispiel beschreibt eine infinite Zahl. Ihr Betrag ist unendlich groß, denn wenn man sie mit irgendeiner reellen Zahl vergleicht, sind immer unendlich viele Folgenglieder größer, aber nur endlich viele kleiner als diese reelle Zahl. Sie ist sogar eine hypernatürliche Zahl, denn die Folgenglieder sind ausschließlich natürliche Zahlen, und diese Eigenschaft überträgt sich ins Unendliche.
Bei der zweiten Folge kann man nicht sofort sagen, welche Zahl sie beschreibt. Für diese Entscheidung spielt die Äquivalenzrelation genügend viel die zentrale Rolle, worauf ich in einem eigenen Tutorial eingehen werde.
F: Du solltest aber schon einmal andeuten, was es mit dieser Äquivalenzrelation auf sich hat.
A: In Ordnung, dann sage ich Dir zunächst, mit welchen Folgen die bisherigen reellen Zahlen beschrieben werden. Es sind dies die konstanten Folgen. Die Folge
(7; 7; 7; 7; 7; 7; 7; 7; …) beschreibt also die reelle 7, und
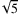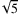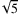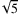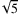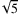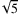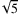(; ; ; ; ; ; ; ; …) ist gleichbedeutend mit .
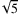Und nun zur Äquivalenzrelation. Beide Zahlen sind kleiner als die Zahl
(1; 2; 3; 4; 5; 6; 7; 8; 9; …),
denn endlich viele Folgenglieder sind kleiner, aber unendlich viele größer. Der gliedweise Vergleich der Zahlenfolgen ergibt also, dass genügend viele Folgenglieder von
(1; 2; 3; 4; 5; 6; 7; 8; 9; …) größer sind als von (7; 7; 7; 7; 7; 7; 7; 7; …),
also ist die mit der ersten Folge beschriebene Zahl die größere. Entsprechendes gilt für 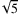und jede andere reelle Zahl, weswegen (1; 2; 3; 4; 5; 6; 7; 8; 9; …) tatsächlich im Unendlichen liegt, also aktual unendlich ist.
Der Vergleich mit (1; 3; 1; 3; 1; 3; 1; 3; 1; …) gelingt aber nicht so einfach, denn man erkennt nicht, ob diese Folge vielleicht für 1, vielleicht für 3 oder vielleicht für eine ganz andere Zahl steht. Aber dazu an anderer Stelle mehr.
F: Ich bin gespannt, wie genügend viel bei Folgen wie (1; 3; 1; 3; 1; 3; 1; 3; 1; …) funktioniert. Es fehlt aber noch die Übertragung der Rechengesetze in die neue Zahlenmenge.
A: Das ist ganz einfach. Mit den Zahlenfolgen rechnet man, indem man die jeweilige Rechenoperation gliedweise ausführt, wie übrigens auch schon bei den reellen Zahlen. Genau wie 7 + 5 = 12 ist nun
(7; 7; 7; 7; 7; 7; 7; 7; …) + {5; 5; 5; 5; 5; 5; 5; 5; …) = {12; 12; 12; 12; 12; 12; 12; 12; …)
Du kannst Dir weitere Beispiele ausdenken.
Ich möchte Dich abschließend auf etwas aufmerksam machen. Betrachte noch einmal die beiden Zahlenfolgen
(1,4; 1,41; 1,414; 1,4142; 1,41421; 1,414213; 1,4142135; 1,41421356; 1,414213562; …)
und
(1,5; 1,42; 1,415; 1,4143; 1,41422; 1,414214; 1,4142136; 1,41421357; 1,414213563; …)
von vorhin. In der Menge der reellen Zahlen beschreiben beide Folgen dieselbe Zahl, nämlich . In der Menge der hyperreellen Zahlen stehen beide Folgen für verschiedene Zahlen, denn sie stimmen in keinem einzigen Folgenglied überein. Subtrahierst Du nun zum Beispiel die erste Folge von der zweiten, dann erhältst Du
(0,1; 0,01; 0,001; 0,0001; 0,00001; 0,000001; 0,0000001; 0,00000001; 0,000000001; …).
Diese Folge kann keinesfalls die hyperreelle 0 beschreiben, denn kein einziges Folgenglied ist gleich null. Du hast hier ein Beispiel für eine infinitesimale Zahl, deren Betrag kleiner als jede reelle Zahl ist, aber eben nicht gleich null. Warum dem wirklich so ist, kannst Du selbst aus dem herausfinden, worüber wir bereits gesprochen haben.
F: Na klar! Bei dieser Folge werden immer unendlich viele Glieder kleiner sein als die bei einer konstanten Folge. Nur endlich viele sind größer oder gleich. Folglich ist die zugehörige Zahl betragsmäßig kleiner als jede reelle Zahl, also infinitesimal. Mir ist auch klar, dass keine der beiden Folgen, die in der Menge der reellen Zahlen die beschreiben, dies bei den hyperreellen Zahlen tut, denn beide sind nicht konstant.
A: Stimmt! Und noch eine weitere Übung habe ich. Gib doch zu allen bisher mit Folgen beschriebenen hyperreellen Zahlen jeweils die Folge der Gegenzahl und des Kehrwertes an. Kannst Du ggf. auch sagen, ob sie infinit, infinitesimal oder keins von beidem sind?
Über die verschiedenen Typen hyperreeller Zahlen werden wir uns aber in einem weiteren Tutorial unterhalten.