„Genügend viel”, „Genügend oft” — Was meint man damit? — Teil 1

F: Wenn von der Konstruktion hyperreeller Zahlen die Rede ist, hört man immer wieder von der Relation „genügend oft”. Wie soll ich das verstehen?
A: Das hängt mit den reellen Zahlenfolgen zusammen, mit denen hyperreelle Zahlen beschrieben werden.
F: Das weiß ich schon: Jede reelle Zahlenfolge beschreibt eine hyperreelle Zahl.
A: Ja, aber nicht jede Folge beschreibt eine eigene Zahl. Um eine bestimmte hyperreelle Zahl zu beschreiben, gibt es immer viele verschiedene Folgen.
F: Ich denke, jede Folge beschreibt ...
A: Achte auf die Formulierung! Wenn es heißt, jede Folge beschreibt eine Zahl, dann bedeutet das, jede nur denkbare Zahlenfolge ist dafür geeignet. Aber verschiedene Folgen können dieselbe Zahl beschreiben. Das ist aber nichts Neues. Denk doch an die Einführung von Bruchzahlen. Man wollte, dass auch Divisionsaufgaben wie 5:7 eine Lösung besitzen. Da hat man die Aufgabe nur auf andere Weise hingeschrieben, nämlich 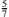und hat festgelegt, das ist die neue Zahl, so soll sie geschrieben werden. Aber auch Divisionsaufgaben wie 10:14 oder 15:21 haben dasselbe Ergebnis wie 5:7. Und da hast Du schon drei Schreibweisen für ein und dieselbe Zahl, nämlich 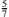, 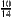und 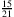. Und Du weißt, dass es noch viele weitere Schreibweisen dafür gibt.
F: Ach so! Diesen Gesichtspunkt, der mit dem Erweitern und Kürzen zusammenhängt, hatte ich übersehen. Bei der Erweiterung zu den irrationalen Zahlen gibt es das ja auch. Zum Beispiel gibt es für 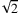viele Intervallschachtelungen.
A: Schön, dass Du Dich jetzt erinnerst. Du siehst also ein, dass es auch für eine hyperreelle Zahl viele beschreibende Folgen gibt. Entscheidend ist aber nun die Frage nach den Kriterien, wann zwei verschiedene Folgen dieselbe hyperreelle Zahl beschreiben.
F: Woran erkennt man denn, dass zwei Folgen dieselbe Zahl beschreiben?
A: Das tun sie, wenn sie genügend oft übereinstimmen. Aber schauen wir uns erst einmal an, wie eine Zahlenfolge aussieht. Sie besteht aus Zahlen, die in einer bestimmten Reihenfolge angeordnet sind. Man kann sie also durchnumerieren. Die erste Zahl hat die Nummer Eins, die zweite die Zwei, die dritte die Drei und so weiter. Eine letzte Nummer gibt es nicht, also kommen bis auf die Null alle natürlichen Zahlen als Index, das ist der Fachbegriff für Nummer, vor. Die Menge aller Indizes ist also .
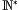F: Verstanden!
A: Zwei Folgen sind dann verschieden, wenn bei mindestens einer Nummer, bei irgendeinem Index, verschiedene Zahlen stehen. Die Frage ist nun, bei wieviel Indizes mit unterschiedlichen Zahlen wird noch dieselbe hyperreelle Zahl beschrieben und bei wie vielen nicht mehr. Was also bedeutet genügend viel Übereinstimmung?
F: Es ist wohl klar, dass zwei Folgen, die übereinstimmen, dieselbe Zahl beschreiben, und wenn sie bei keinem Index übereinstimmen, sie verschiedene Zahlen beschreiben.
A: Richtig! Aber wie groß muss die Teilmenge von 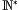sein, damit die beiden Folgen dieselbe Zahl beschreiben? Nimm einmal die Folgen
(2 ; 2 ; 5 ; 5 ; 5 ; 5 ; 5 ; 5 ; ...) und
(7 ; 7 ; 7 ; 2 ; 2 ; 2 ; 7 ; 7 ; ...).
Sie setzen sich ausschließlich mit Fünfen bzw. Siebenen fort. Wären sie geeignet, die Zahl 2 zu beschreiben?
F: Ich glaube nicht, denn in beiden Folgen stehen nur endlich viele Zweien.
A: Natürlich hast Du recht, denn würden beide Folgen die 2 beschreiben, wären sie beide äquivalent, also gleichwertig, obwohl sie bei keinem einzigen Index übereinstimmen. Und dies hatten wir soeben als nicht äquivalent erkannt. Was schließt Du daraus?
F: Naja, endlich viele Unterschiede bei zwei Folgen sind nicht genügend viel, um von verschiedenen hyperreellen Zahlen zu sprechen. Oder umgekehrt: Unterscheiden sich zwei Folgen nur an endlich vielen Stellen, so beschreiben sie dieselbe Zahl. Also ist
(2 ; 2 ; 5 ; 5 ; 5 ; 5 ; 5 ; 5 ; ...) gleichwertig zu
(5 ; 5 ; 5 ; 5 ; 5 ; 5 ; 5 ; 5 ; ...) und
(7 ; 7 ; 7 ; 2 ; 2 ; 2 ; 7 ; 7 ; ...) gleichwertig zu
(7 ; 7 ; 7 ; 7 ; 7 ; 7 ; 7 ; 7 ; ...).
A: Gut! Dann betrachten wir jetzt die Folgen
(0 ; 1 ; 0 ; 1 ; 0 ; 1 ; 0 ; 1 ; ...) und
(1 ; 0 ; 1 ; 0 ; 1 ; 0 ; 1 ; 0 ; ...).
F: Setzen sich die Folgenglieder auf diese Weise fort?
A: Ja.
F: Bei keinem Index stimmen die Folgen überein, also beschreiben sie verschiedene Zahlen.
A: Richtig! Dann addiere und multipliziere doch einmal beide Zahlen. Du weißt, das musst Du gliedweise bei übereinstimmenden Indizes tun.
F: Naja,
(0 ; 1 ; 0 ; 1 ; 0 ; 1 ; 0 ; 1 ; ...) + (1 ; 0 ; 1 ; 0 ; 1 ; 0 ; 1 ; 0 ; ...) = (1 ; 1 ; 1 ; 1 ; 1 ; 1 ; 1 ; 1 ; ...) und
(0 ; 1 ; 0 ; 1 ; 0 ; 1 ; 0 ; 1 ; ...) ⋅ (1 ; 0 ; 1 ; 0 ; 1 ; 0 ; 1 ; 0 ; ...) = (0 ; 0 ; 0 ; 0 ; 0 ; 0 ; 0 ; 0 ; ...).
Die Summe ist gleich 1, und das Produkt ist gleich 0. ... Ist ein Produkt gleich null, dann ist mindestens einer seiner Faktoren gleich null. ... Aber welcher ...?
A: Beachte noch, dass die Summe der beiden Zahlen gleich eins ist. Es kann also nur eine der beiden Folgen die Null beschreiben.
F: Und die jeweils andere dann automatisch die Eins. ... Beide Folgen enthalten unendlich viele Nullen und unendlich viele Einsen, aber bei keinem Index stimmen sie überein. ...
A: Was meinst Du, welche Folge die Null und welche die Eins beschreibt?
F: Das kann ich nicht erkennen. Vielleicht kann man an dieser Stelle selbst festlegen, welche Folge für welche Zahl steht.
A: Genauso macht man es auch! Aber wenn Du einmal eine Festlegung getroffen hast, dann gilt sie für alle Folgen. Entscheidest Du Dich dafür, dass
(0 ; 1 ; 0 ; 1 ; 0 ; 1 ; 0 ; 1 ; ...) = (1 ; 1 ; 1 ; 1 ; 1 ; 1 ; 1 ; 1 ; ...) ist,
dann hast Du automatisch festgelegt, dass alle geraden Indizes genügend viel bedeutet. Stimmen also zwei Folgen bei allen geraden Indizes überein, dann beschreiben sie dieselbe hyperreelle Zahl. Dann muss auch
(1 ; 0 ; 1 ; 0 ; 1 ; 0 ; 1 ; 0 ; ...) = (0 ; 0 ; 0 ; 0 ; 0 ; 0 ; 0 ; 0 ; ...) sein. Alle ungeraden Indizes zusammengenommen sind dann nicht genügend viel ...
F: Unendlich viele Indizes können also nicht genügend viele sein?
A: Ja, das mag zwar verwirren, aber es ist richtig. Die anderen unendlich vielen reichen aus, um genügend viel zu sein.
F: Was mich ein wenig verwirrt, ist, dass ich nur noch halb so viele ...
A: Falsch! Bedenke bitte, dass es immer noch unendlich viele Folgenglieder sind, die die Folgen als 1 bzw. 0 festlegen. Die Vorstellung aus dem Endlichen, man hätte die Hälfte der Folgenglieder weggenommen, kann man nicht ins Unendliche übertragen. Alle geraden Folgenglieder zusammengenommen sind genauso viele wie alle Folgenglieder zusammen, nämlich unendlich viele.
F: Ach ja?... Du hast recht, denn beim Durchzählen der geraden Folgenglieder wird man genausowenig fertig wie beim Durchzählen aller Folgenglieder oder der ungeraden. Also haben wir durch das Wegnehmen unendlich vieler Folgenglieder gar nicht weniger als vorher. Das Unendliche überrascht immer wieder ...
A: Gehen wir noch einen Schritt weiter und betrachten Folgen mit einem Dreierrhythmus aus Nullen und Einsen. Hier hast Du alle sechs Möglichkeiten, und ich habe allen Folgen, also den Zahlen, gleich Namen gegeben, damit wir leichter darüber sprechen können:
g = (0; 0; 1; 0; 0; 1; 0; 0; 1; 0; 0; 1; 0; 0; 1; 0; 0; 1; 0; 0; 1; 0; 0; 1; ...)
h = (0; 1; 0; 0; 1; 0; 0; 1; 0; 0; 1; 0; 0; 1; 0; 0; 1; 0; 0; 1; 0; 0; 1; 0; ...)
i = (1; 0; 0; 1; 0; 0; 1; 0; 0; 1; 0; 0; 1; 0; 0; 1; 0; 0; 1; 0; 0; 1; 0; 0; ...)
j = (1; 1; 0; 1; 1; 0; 1; 1; 0; 1; 1; 0; 1; 1; 0; 1; 1; 0; 1; 1; 0; 1; 1; 0; ...)
k = (1; 0; 1; 1; 0; 1; 1; 0; 1; 1; 0; 1; 1; 0; 1; 1; 0; 1; 1; 0; 1; 1; 0; 1; ...)
l = (0; 1; 1; 0; 1; 1; 0; 1; 1; 0; 1; 1; 0; 1; 1; 0; 1; 1; 0; 1; 1; 0; 1; 1; ...)
F: Warum nimmst Du eigentlich immer Folgen, die nur aus Nullen und Einsen bestehen? Es gibt doch noch ganz andere Folgen mit solchen Rhythmen.
A: Natürlich hast Du recht. Der Grund ist, dass man an ihnen anschaulich zeigen kann, dass unendlich viele Folgenglieder nicht genügend viel sein können.
F: Ich glaube, jetzt könnte man mit paarweiser Addition und Multiplikation wieder herausfinden, welche Produkte gleich null und welche Summen gleich eins sind. Man hätte dann wieder die Freiheit, eine Zahl als Null zu definieren, woraus sich die Werte der anderen ergeben.
A: Richtig! Und ich gebe Dir hiermit gleich die neun interessanten Summen und Produkte, bei denen ausschließlich Nullen oder Einsen als Folgenglieder auftreten. Die anderen Rechnungen solltest Du durchaus noch selbst durchführen. Hier sind nun die errechneten Zahlenfolgen. Beim Hinschreiben habe ich berücksichtigt, dass wir die Folgenglieder mit ungeraden Indizes bereits als nicht genügend viel erklärt haben. Auf die kommt es also nicht mehr an.
(1) g ⋅ h = (0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; ...)
(2) g ⋅ i = (0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; ...)
(3) g + j = (1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; ...)
(4) g ⋅ j = (0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; ...)
(5) h ⋅ i = (0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; ...)
(6) h + k = (1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; ...)
(7) h ⋅ k = (0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; ...)
(8) i + l = (1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; ...)
(9) i ⋅ l = (0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; ...)
F: Alle Zahlen g bis l können ja nur entweder Eins oder Null bedeuten. Die Gleichungen (3) und (4) sind wieder so wie bei den Folgen mit Zweierrhythmus. Ich nehme einmal g=0 und j=1 an. ... Da komme ich nicht weiter, weil in den Gleichungen (1) und (2) die Zahlen h und i sowohl gleich 1 als auch gleich 0 sein können. Und die anderen Gleichungen liefern keine weiteren Informationen.
Also setze ich jetzt g=1 und j=0. ... Ah, jetzt komme ich weiter. Aus Gleichung (1) folgt h=0 und aus Gleichung (2) schließlich i=0. Dann ergibt sich aus Gleichung (6) k=1 und aus Gleichung (8) l=1. Fertig!
A: In Ordnung! Bitte untersuche nun, ob das mit den ursprünglichen Folgen mit den sechs Zahlen g bis l harmoniert.
F: Hm! ... Wenn ich genau hinschaue, dann stimmen meine Ergebnisse jeweils mit den 3., 6., 9. usw. Folgengliedern überein, wenn also die Indizes durch 3 teilbar sind.
A: Richtig! Würdest Du mit den anderen Gleichungen die Probe machen, ergäben sich übrigens keine Widerspüche, auch nicht bei den Gleichungen, die ich Dir nicht aufgeschrieben habe.
Und ich will Dir noch etwas sagen. Wenn Du mit den Gleichungen (6) und (7) angefangen hättest, dann hättest Du Übereinstimmung bei den Indizes 3n-1 gefunden, und bei der dritten Möglichkeit, nämlich mit den Gleichungen (8) und (9) anzufangen, bei den Indizes 3n-2. Probiere es ruhig aus!
Aber jetzt bleiben wir bei Deinem Ergebnis. Wir sind doch beim Thema „genügend viel”.
F: Dann würde ich sagen, dass bei diesen Folgen bereits alle Folgenglieder mit durch drei teilbaren Indizes genügend viel sind, um zu erkennen, dass zum Beispiel
(0; 0; 1; 0; 0; 1; 0; 0; 1; 0; 0; 1; 0; 0; 1; ...) = (1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; ...) ist.
A: Richtig! Und das ist dann bei allen denkbaren reellen Zahlenfolgen so. Bereits alle Folgenglieder mit durch 3 teilbaren Indizes sind genügend viele, und das sind immer noch unendlich viele. Und nun pass auf! Bei den Zahlenfolgen im Zweierrhythmus haben wir festgelegt, dass alle geraden Indizes bereits genügend viele Folgenglieder ergeben, was für alle Folgen zu gelten hat ...
F: Dann sind ja bereits alle Folgenglieder mit durch sechs teilbaren Indizes genügend viel. Wie weit soll denn das noch gehen? Es gibt doch auch Zahlenfolgen im Vierer-, Fünfer, Sechserrhythmus usw. und noch viele andere ...
A: ... Und man streicht immer mehr Indizes weg. Aber es bleiben unendlich viele übrig, und das sind dann immer noch genügend viel.
F: Und Du bist sicher, dass das funktioniert? Bleiben wirklich unendlich viele Folgenglieder als genügend viel übrig?
A: Ich will Dir ein Beispiel geben, mit dem Du sicherlich vertraut bist. Stelle Dir bitte die Menge 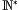vor. Nun streichst Du zunächst die 1 weg, und anschließend streichst Du alle Zahlen weg, die Vielfache einer anderen Zahl sind. Bleibt da irgendeine Zahl übrig?
F: Ja, natürlich bleiben alle Primzahlen übrig. ... Und davon gibt es unendlich viele. Du hast recht. So verhält es sich also auch bei den Folgen reeller Zahlen, die hyperreelle Zahlen beschreiben. Habe ich es nun richtig verstanden? Zwei Folgen beschreiben die Null, wenn bei geraden Indizes jeweils eine Null steht. Zwei andere Folgen beschreiben die Null, wenn bei durch drei teilbaren Indizes jeweils eine Null steht. Dann kann man natürlich sagen, dass bei zwei Folgen, die bei durch sechs teilbaren Indizes eine Null besitzen, sie ebenfalls die Null beschreiben.
A: So ist es. Verallgemeinert heißt das, dass zwei Folgen dieselbe Zahl beschreiben, wenn ihre Folgenglieder an allen durch sechs teilbaren Indizes übereinstimmen.
F: Und so wird man, wenn man auch andere Arten von Folgen einbezieht, vielleicht auch fertig. Aber was wäre denn, wenn wir beim ersten Beispiel festgelegt hätten, dass alle ungeraden Indizes genügend viel seien ...
A: ... und beim zweiten Beispiel vielleicht die Indizes 3n-1 als genügend viel festgelegt hätten? Dann stünden fortan zwei Folgen für dieselbe Zahl, wenn sie bei Indizes überstimmen, die ungerade sind und das Kriterium 3n-1 erfüllen. Das sind dann die Indizes 5, 11, 17, 23 und so weiter.
F: Aber kann denn das funktionieren? Da erklärt der eine Mathematiker alle Indizes 6, 12, 18, 24 usw. als genügend viel und ein anderer Mathematiker alle Indizes 5, 11, 17, 23 usw. als genügend viel. Und ein dritter nimmt eine dritte Variante? Das kann doch nicht richtig sein.
A: Ich merke schon, dass Du hartnäckig bist. Und Dein Nachfragen ist ja berechtigt. Die entscheidende Frage ist doch, ob dann, wenn alle Mathematiker alle Varianten von Folgen verarbeitet haben, jeder von ihnen bei einer endgültigen Menge von Indizes ankommt, die dann als genügend viel gilt. Das bedeutet übrigens nicht, dass sie alle bei derselben endgültigen Indexmenge ankommen müssen.
Noch einmal: Es ist nur zu beweisen, dass es geht, mehr nicht!
Und wie man das beweist, das will ich Dir dann auch noch schildern.
F: Ja, bitte!
A: Aber das machen wir im zweiten Teil dieses Tutorials.