Tutorials zur Nichtstandard-Analysis
Hyperreelle Zahltypen und woran man sie erkennt
F: Wie schreibt man denn infinite oder infinitesimale Zahlen auf? Eine Zahlenfolge hinzuschreiben, ist ja unpraktisch. Außerdem kann ich ohnehin immer nur einen Folgenanfang hinschreiben und somit nie die „komplette“ Zahl.A: Bereits hinter den irrationalen Zahlen verbergen sich Folgen, wie wir in unserem Tutorial über Zahlbereichserweiterungen bereits erkannt haben.
F: Ja, ich weiß. Aber statt einer Folge von Intervallen bzw. Intervallgrenzen schreibt man zum Beispiel
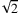 als Kurzform. Außerdem erkennt man an dieser Schreibweise, dass ihr Quadrat gleich 2 sein soll. Ich denke, aus praktischen Gründen sollte es auch für Folgen wie
(1; 2; 3; 4; 5; 6; 7; 8; 9; …)
eine Kurzschreibweise geben, die das Rechnen erleichtert.
als Kurzform. Außerdem erkennt man an dieser Schreibweise, dass ihr Quadrat gleich 2 sein soll. Ich denke, aus praktischen Gründen sollte es auch für Folgen wie
(1; 2; 3; 4; 5; 6; 7; 8; 9; …)
eine Kurzschreibweise geben, die das Rechnen erleichtert.A: Die Zahl, die mit der speziellen Folge aller natürlichen Zahlen beschrieben wird, hat tatsächlich eine besondere Bezeichnung, nämlich
 . Sie ist eine hypernatürliche Zahl und infinit. Die um 8 größere Zahl ist
. Sie ist eine hypernatürliche Zahl und infinit. Die um 8 größere Zahl ist
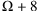 , ihr Dreifaches
, ihr Dreifaches 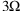 , die Hälfte
, die Hälfte 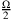 und ihre dritte Potenz
und ihre dritte Potenz 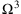 . Das ist doch ganz einfach.
. Das ist doch ganz einfach.F: Verwendet man also Buchstaben zur Bezeichnung infiniter Zahlen? Da könnte man doch denken, es handelt sich um eine Variable. Bei irrationalen Zahlen benutzt man aber spezielle Schreibweisen wie
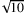 oder ln(3).
oder ln(3).A: Aber auch bei
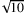 heißt die um 8 größere Zahl
heißt die um 8 größere Zahl 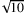 + 8 usw. …
+ 8 usw. …F: Deine Antwort befriedigt mich noch nicht. Gibt es denn zum Beispiel für die Zahl, die zur Folge (3; 4; 6; 7; 9; 10; 12; 13; 15; …) gehört, auch nur einen Buchstaben als Kurzzeichen?
A: Nein, das gibt es nicht. Ich will Dich auch nicht weiter auf die Folter spannen. Für die Analysis der reellen Funktionen genügt es nämlich zu wissen, ob eine Zahl infinit ist oder nicht, ob sie infinitesimal ist oder nicht. Deshalb benötigt man auch keine spezielle Schreibweise wie bei
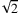 oder ln(3), die angibt, wo man die Zahl auf der Zahlengeraden suchen muss. Infinite Zahlen liegen immer jenseits aller reellen Zahlen.
oder ln(3), die angibt, wo man die Zahl auf der Zahlengeraden suchen muss. Infinite Zahlen liegen immer jenseits aller reellen Zahlen.Wichtig ist aber, an einem Term, in welchem infinite oder infinitesimale Zahlen oder beides vorkommen, zu erkennen, was für einen Typ von hyperreeller Zahl er beschreibt. Man hat daher zweckmäßigerweise festgelegt, welche Art von Buchstaben man jeweils für die Zahltypen benutzt.
So verwendet man für infinite Zahlen große griechische Buchstaben. Das hast Du an der speziellen Zahl
 vielleicht schon bemerkt. Ansonsten nimmt man die Buchstaben vom Anfang des griechischen Alphabets, also Α, Β, Γ, Δ und so weiter. Man sollte aber aufpassen, dass die Symbole nicht mit lateinischen Buchstaben verwechselt werden können. Α und Β sind also ungünstig, sie lassen sich aber nicht immer vermeiden.
vielleicht schon bemerkt. Ansonsten nimmt man die Buchstaben vom Anfang des griechischen Alphabets, also Α, Β, Γ, Δ und so weiter. Man sollte aber aufpassen, dass die Symbole nicht mit lateinischen Buchstaben verwechselt werden können. Α und Β sind also ungünstig, sie lassen sich aber nicht immer vermeiden.F: Wieso kann man sie denn nicht vermeiden?
A: Weil man gerne gewisse strukturelle Merkmale erkennen will. Für den Kehrwert der Zahl
 , also
, also 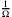 , nimmt man den entsprechenden Kleinbuchstaben ω. Diese Zahl wird also von der Folge
(1;
, nimmt man den entsprechenden Kleinbuchstaben ω. Diese Zahl wird also von der Folge
(1;
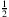 ;
;
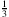 ;
;
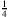 ;
;
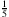 ;
;
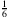 ;
;
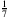 ;
;
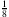 ;
;
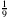 ;
…)
beschrieben. ω ist offensichtlich eine infinitesimale Zahl. Und da verstehst Du sicherlich die Festlegung, dass man ganz allgemein für infinitesimale Zahlen griechische Kleinbuchstaben wie α, β, γ, δ und so weiter verwendet.
;
…)
beschrieben. ω ist offensichtlich eine infinitesimale Zahl. Und da verstehst Du sicherlich die Festlegung, dass man ganz allgemein für infinitesimale Zahlen griechische Kleinbuchstaben wie α, β, γ, δ und so weiter verwendet.Hat man für eine Infinitesimalzahl erst einmal den Buchstaben α verwendet, dann bleibt nichts anderes übrig, als den zugehörigen Kehrwert mit Α zu bezeichnen.
F: Haben wir jetzt alle hyperreellen Zahltypen?
A: Nein, noch nicht. Zunächst gibt es noch die bekannten reellen Zahlen mit den bekannten Schreibweisen, die einen Teilkörper von
 bilden. Da aber die üblichen Rechengesetze innerhalb von
bilden. Da aber die üblichen Rechengesetze innerhalb von  (manchmal auch als
(manchmal auch als 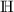 bezeichnet) gelten, muss es auch Zahlen wie 5 + α oder 7 − 5α geben. Solche Zahlen sind weder reell noch infinitesimal noch infinit. 5 + α ist infinitesimal benachbart zur 5 und 7 − 5 infinitesimal benachbart zur 7. Da sie nicht infinit sind, bezeichnet man sie als finit.
bezeichnet) gelten, muss es auch Zahlen wie 5 + α oder 7 − 5α geben. Solche Zahlen sind weder reell noch infinitesimal noch infinit. 5 + α ist infinitesimal benachbart zur 5 und 7 − 5 infinitesimal benachbart zur 7. Da sie nicht infinit sind, bezeichnet man sie als finit.F: Einen Moment bitte! Du bezeichnest 5 + α als finit, weil diese Zahl nicht infinit ist. Reelle Zahlen und infinitesimale Zahlen sind aber ebenfalls nicht infinit …
A: Du hast gut aufgepasst. Man unterscheidet also die beiden Typen infinite Zahlen einerseits und finite Zahlen andererseits. Bei den letzteren gibt es noch die beiden speziellen Untertypen reelle Zahlen und infinitesimale Zahlen.
Die Zahlenmengen dieser beiden Untertypen sind nicht einmal disjunkt. Fällt Dir eine reelle Zahl ein, die zugleich infinitesimal ist?






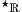 – Teil 1
– Teil 1