Sir Isaac Newton (1642 bis 1727)

Sir Isaac Newton wurde, nach dem damals gültigen julianischen Kalender, am 25. Dezember 1642 in Woolsthorpe in Lincolnshire geboren und starb am 20. März 1727 in Kensington. Als im Jahre 1752 auch in England der gregorianische Kalender eingeführt wurde, änderten sich diese Daten auf den 4. Januar 1643 bzw. 31. März 1727.
Newton gilt als einer der bedeutendsten Wissenschaftler aller Zeiten, vor allem ist er wegen seiner Leistungen in der Physik und der Mathematik berühmt. Er verfasste die "Philosophiae Naturalis Principia Mathematica", das als eines der wichtigsten wissenschaftlichen Werke gilt. Darin beschrieb er mit seinem Gravitationsgesetz die universelle Gravitation und entwickelte schließlich die Bewegungsgesetze.
Er war damit Begründer der klassischen Mechanik, welche ohne die Infinitesimalmathematik kaum zu entwickeln gewesen wäre. Deren Vorläufer hatte er 1666 als Manuskript niedergeschrieben, veröffentlichte sie aber erst im Jahre 1704. Mit Gottfried Wilhelm Leibniz, der etwa zur gleichen Zeit wie Newton die Infinitesimalrechnung entwickelt hatte, entstand daher ein Prioritätenstreit, wer deren "eigentlicher" Erfinder gewesen war. Heute schreibt man beiden die Urheberschaft zu.
Auch Newton hatte, genau wie Leibniz, erkannt, dass die Methoden, einerseits Flächeninhalte und andererseits Steigungen von Kurven zu bestimmen, invers zueinander sind.
Isaac Newton war viele Jahre lang Inhaber des berühmten Lucasischen Lehrstuhls für Mathematik am Trinity College der Universität Cambridge. Er lieferte wesentliche Beiträge zur Optik (Korpuskeltheorie, Lichtbrechung, Erklärung des Spektrums), auch verallgemeinerte er den binomischen Lehrsatz mittels unendlicher Reihen auf beliebige reelle Exponenten. Man kann ihn wegen seiner Forschungen auf vielen Gebieten als Philosophen bezeichnen.
Hier soll sein Beitrag zur Infinitesimalrechnung im Vordergrund stehen.

Das Ableiten von Funktionen nach Newton

Die Idee der Fluxionen

Newton geht an Kurven nicht vom geometrischen Standpunkt heran, sondern sieht sie als die Spur eines in der Ebene bewegten Punktes. Wie bei einem heutigen Plotter ist der Zeichenpunkt als Schnittpunkt zweier zu einander senkrecht stehender Geraden definiert. Beide Geraden lassen sich unabhängig von einander parallel zu sich selbst verschieben. Bei Kenntnis der beiden Verschiebungsfunktionen x(t) und y(t) ist die Lage des Zeichenpunktes P(t) zu jedem Zeitpunkt t zu ermitteln, d. h. die Kurve zu beschreiben.

Weil Newton die Bewegung beim Zeichnen einer Kurve in den Mittelpunkt stellt, ergibt sich für ihn die Frage nach der Zeichengeschwindigkeit. Wie ein Fußgänger schon auf geradem Wege bald schneller, bald langsamer gehen kann, so ist die Veränderlichkeit der Geschwindigkeit bei gekrümmten Wegen auch noch hinsichtlich der Richtung von Bedeutung.
Deshalb ist die vektorielle Darstellung mittels des Ortsvektors von P(t) das geeignete Hilfsmittel zur Darstellung der newtonschen Gedanken:



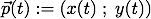
Ähnlich wie man die Kurve dadurch überschaut, indem man zu jedem Zeitpunkt angeben kann, wo der Zeichenpunkt ist, so möchte Newton den Geschwindigkeitsvektor 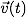zu jedem Zeitpunkt t kennen. Und das müsste aus dem Zeichenvorgang, d.h. aus (x(t) ; y(t)) zu ermitteln sein.

Aber der Begriff "Geschwindigkeit zu einem Zeitpunkt" ist problematisch, denn schon Zenon von Elea (490 bis 430 v. Chr) argumentierte, dass ein Pfeil eigentlich nicht fliegen könne, weil er ja zu jedem Zeitpunkt an einer ganz bestimmten Stelle ruhe. Newton löste diese Problematik mit dem Begriff der Momentangeschwindigkeit. Dabei lässt sich ein Moment mittels hyperreeller Zahlen als eine infinitesimale Zeitspanne dt modellieren.
(Anmerkung: Die Leibniz-Schreibweise "dt" wird hier benutzt, um mit den übrigen Abschnitten leichter vergleichen zu können.)

Newton geht nun von der Grundannahme aus:
In jedem Moment verläuft jede Bewegung geradlinig und gleichförmig.



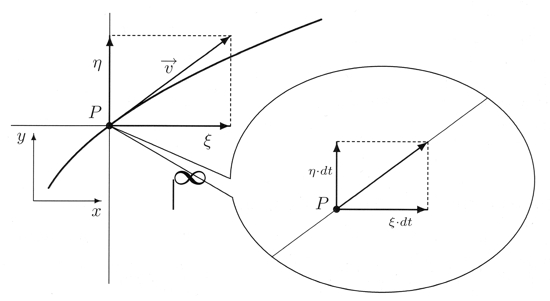
In der Abbildung wird z.B. mit einem infiniten Faktor 1/dt vergrößert, um die Vorstellung der Momentangeschwindigkeit geometrisch wiederzugeben.
In der Spanne dt wird die senkrechte Gerade um ξ·dt und gleichzeitig die horizontale Gerade um η·dt gleichförmig weiterbewegt. Die Proportionalitäts-
faktoren ξ und η sind die in der Zeitspanne dt konstanten Zeichengeschwindig-
keiten in x- bzw. y-Richtung und natürlich vom Zeitpunkt t₀ abhängig, was Newton in den Formeln nicht explizit notierte. Die geradlinig gleichförmige Bewegung des Schnittpunktes wird dann beschrieben durch



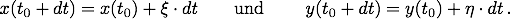
Die Faktoren ξ und η nennt Newton Fluxionen, weil der Zeichenprozess im "Flusse der Zeit" abläuft. Er geht davon aus, dass es sich dabei selbstverständlich um "normale" Zahlen, also um heutige reelle Zahlen handeln muss. Demzufolge lässt sich schreiben



Daraus folgt sofort für den Differenzialquotienten von Leibniz



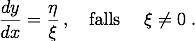
(Anmerkung: Dieser enge Zusammenhang zwischen Differenzialen und Fluxionen hat zu dem unerfreulichen Prioritätenstreit zwischen Leibniz und Newton geführt.)

Newton bestimmt also Differenzialquotienten nur mit reellem Zähler und Nenner, den Fluxionen ξ und η. Für infinitesimale Zahlen sorgt dann ein Moment dt, dt ≠ 0,



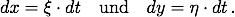
Damit ist vorgegeben, wie beide Koordinaten des gesuchten Geschwindigkeits-
vektors 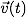zu bestimmen sind:

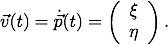
Ein Beispiel für Newtons Fluxionsrechnung

Gegeben sei eine Parabel mittels x(t) = 2t und y(t) = 8t², also parameterfrei
y = 2x². Gesucht ist die entsprechende Gleichung für die Fluxionen ξ und η.
Zunächst soll nur Newtons "Rezept" (Begründung dazu siehe unten) befolgt werden:

(0) Set all y^e termes on one side of y^e equation that they become equal to nothing.



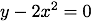
(1) First multiply each terme by so many times ξ/x as x hath dimensions in that terme.



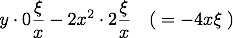
(2) Secondly multiply each terme by so many times η/y as y hath dimensions in it.



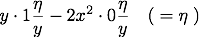
(3) ... the summe of all these products shall bee equal to nothing.



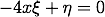
W^ch Equation gives y^e relation of y^e velocitys.

Der Geschwindigkeitsvektor ist damit gefunden:



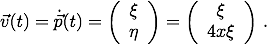
Damit gilt:

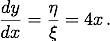
Begründung der Fluxionsregel

Die beiden bisherigen Beispiele gehören zu der recht umfangreichen Menge aller Kurven, die mittels eines polynomialen Zusammenhanges zwischen den Koordinatenfunktionen x und y beschrieben werden. Newton stellte sich allgemein die Aufgabe:
Gegeben ist eine Gleichung zwischen x und y mit einer endlichen Summe:



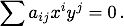
Gesucht ist die zugehörige Beziehung zwischen den Fluxionen ξ und η.
Seine Grundidee ist, dass die vorgegebene Gleichung für "die fließende Zeit" t besteht, also nicht nur für einen reellen Zeitpunkt t₀, sondern auch für jeden Zeitpunkt t₀ + dt mit infinitesimalem, von null verschiedenem dt.



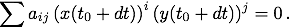
Wegen der geradlinig gleichförmigen Bewegung innerhalb der Zeitspanne dt gilt demnach



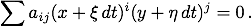
Jeder Summand in dieser Gleichung enthält also ein Produkt zweier Binome, wobei die Exponenten i und j natürliche Zahlen sein sollen. Die Kenntnis der Binomialentwicklung wird hier vorausgesetzt. Es gilt dann



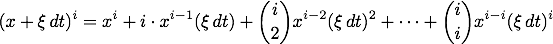
und die entsprechende Gleichung für die y-Koordinaten



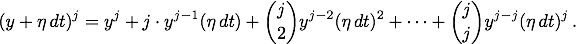
Newton bildet jetzt das Produkt und erhält





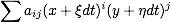
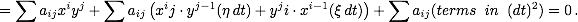
Die drei Summen müssen also insgesamt null ergeben. Die erste Summe ist selbst null, wie ein Blick auf die gegebene Gleichung der Kurve zeigt. Die beiden anderen Summen lassen sich durch den infinitesimalen Faktor dt, dt ≠ 0, dividieren, so dass Newton erhält:



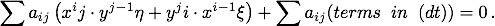
In jedem Summanden der zweiten Summe ist der infinitesimale Faktor dt enthalten, die Summe besteht also aus endlich vielen infinitesimalen Summanden und ist daher selbst infinitesimal. Newton lässt sie als unerheblich fort.
(Anmerkung: Als infinitesimaler Anteil einer hyperreellen Zahl trägt sie zum reellen Teil nichts bei. Newton schrieb in diesem Zusammenhang intuitiv von "gerade verschwindenden Größen". Das hat ihm den Spott von Bischof George Berkeley eingebracht: "May we not call them the ghosts of departed quantities?")

Die restliche Summe formt Newton noch um zu



und teilt das Ergebnis als Gebrauchsanweisung mit:

Fluxionsregel:
Set all y^e termes on one side of y^e equation that they become equal to nothing.
First multiply each terme by so many times ξ/x as x hath dimensions in that terme.
Secondly multiply each terme by so many times η/y as y hath dimensions in it.
[...] the summe of all these products shall bee equal to nothing.
W^ch Equation gives y^e relation of y^e velocitys.

(Quelle: Isaac Newton, The October 1666 Tract on Fluxions)

Weitere Differenziationsregeln und Beispiele zur Fluxionsrechnung finden Sie in unserem --> Buch zur Nichtstandard-Analysis.