Nichtstandard-Analysis für Schulen

Leonhard Euler (1707 bis 1783)

Leonhard Euler wurde am 15 April 1707 in Basel geboren, wo er auch zur Schule ging. Zusätzlich erhielt er Privatunterricht bei Johannes Burckhardt, einem mathematikbegeisterten Theologen. Bereits 1720 begann er an der Universität Basel zu studieren. Unter anderem hörte er hier Vorlesungen von Johann Bernoulli.
Auch mit anderen Angehörigen dieser berühmten Mathematikerfamilie hatte Euler mehrfach zu tun. So berief ihn Daniel Bernoulli 1727 an die Universität St. Petersburg, wo er den Lehrstuhl von Nikolaus II. Bernoulli übernahm. Im Jahre 1730 wurde Euler dort Professor für Physik, 1733 schließlich folgte er Daniel Bernoulli auf dessen Lehrstuhl für Mathematik.
Friedrich der Große berief ihn an die Königlich-preußische Akademie der Wissenschaften in Berlin, wo Euler von 1741 bis 1766 wirkte. Nach dieser Zeit ging er wieder an die Kaiserlich-russische Akademie der Wissenschaften nach St. Petersburg zurück. Euler starb am 18. September 1783 in St. Petersburg, wo auch sein Grab auf dem Lazarus-Friedhof des Alexander-Newski-Klosters liegt.

Leonhard Euler hinterließ ein sehr umfangreiches Werk, nicht allein auf dem Gebiet der Mathematik, aber er schuf in vielen anderen Bereichen mathematische Grundlagen, so z. B. mit seiner Musiktheorie. Für die Physik lieferte er Beiträge zur Hydromechanik und zur Kreiseltheorie. Seine Knickformel war eine Beschreibung für die Belastbarkeit von Stäben. Mit seinen Grundsätzen der Artillerie machte er den Einfluss des Luftwiderstandes auf die Flugbahn eines Geschosses berechenbar. Auch zur Optik lieferte er wesentliche Beiträge.

Viele noch heute verwendete Symbole wie

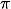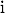, das Summenzeichen Σ und f(x) als Bezeichnung eines Funktionsterms gehen auf Euler zurück. In seinem Grundlagenwerk "Introductio in Analysin Infinitorum" (1748 veröffentlicht) spielte erstmals der Funktionsbegriff eine zentrale Rolle. In dieser "Einleitung in die Analysis des Unendlichen" beschreibt er u. a., wie man die Zahl "e" findet. (Er wählte diese Bezeichnung übrigens als Abkürzung für Exponentialbasis.)

Der Begriff Analysis in der Übersetzung des Buchtitels ist aber nicht im heutigen Sinne zu verstehen, sondern eher wie Analyse. Aus diesem Buch soll im folgenden zitiert werden, wie Euler diese Exponentialbasis mit Hilfe der unendlichen Reihe begründet (in moderner Schreibweise):
e := RT[1 + 1/1! + 1/2! + 1/3! + 1/4! + ... + 1/N!] = RT [(1 + 1/N)^N].
Darin beeindruckt, wie sicher er mit unendlichen Größen rechnet, ohne dass diese zuvor definiert worden sind. Letzteres gelang erst Abraham Robinson ca. zweihundert Jahre später.

Die Berechnung von e nach Euler

Im Gegensatz zu den Potenzfunktionen mit y = xⁿ, bei denen die unabhängige Variable x die Basis ist, bilden die Potenzen zu einer festen Basis a, a > 0, die Exponentialfunktionen mit y = a^x. Wegen a^mx = (a^m)^x, kann jede andere Exponentialfunktion mit y = c^x mittels der Basis a dargestellt werden, es muss nur die passende Zahl m bestimmt werden, sodass a^m = c ist. Das ist eindeutig möglich, weil jede Exponentialfunktion streng monoton ist und nur positive Werte besitzt.
Man kann sich daher auf eine einzige Exponentialfunktion konzentrieren. Als von zentraler Bedeutung hat sich die e-Funktion erwiesen, das ist die Exponentialfunktion, deren Basis die Zahl e ist.
Den einzelnen Paragraphen, die nun aus Eulers Werk zitiert werden (s.o.), folgt jeweils unmittelbar deren Interpretation aus heutiger Sicht mit der Kenntnis infinitesimaler und infiniter Zahlen.

"§ 114
Da a⁰ = 1 ist, und mit wachsendem Exponenten zugleich auch der Wert der Potenz zunimmt, falls a eine Zahl grösser als 1 ist, so folgt daraus, dass, wenn der Exponent unendlich wenig grösser ist als 0, auch die Potenz die Einheit nur um unendlich wenig übersteigen wird. Ist daher ω eine unendlich kleine Zahl [...], jedoch von 0 verschieden, so wird a^ω = 1 + ψ, wenn ψ ebenfalls eine unendlich kleine Zahl bedeutet; [...]. Es ist somit entweder ψ = ω oder ψ > ω oder ψ < ω und zwar wird dies offenbar von der Grösse von a abhängen. Da nun a noch unbekannt ist, so wollen wir ψ = kω setzen. [...]"

In §114 legt Euler fest, von welchen Voraussetzungen er bei seiner Untersuchung der Exponentialfunktionen ausgeht. Zunächst beschränkt er sich auf streng monoton steigende Funktionen und wählt daher a > 1. Ferner wird die Funktion an der Stelle 0 als stetig vorausgesetzt, denn zu jeder infinitesimalen, von null verschiedenen Änderung h der x-Werte, h = ω, soll die Änderung v der Funktionswerte v = ψ = k·ω sein, und es gilt a^ω = 1 + kω. Damit ist eine Exponentialfunktion überall stetig, denn ändert man x infinitesimal zu x + h, dann wird die Änderung der Funktionswerte ebenfalls infinitesimal. Es gilt nämlich
v = a^x+h - a^x = a^xa^h - a^x = a^x(1 + h) - a^x = a^x·kh.

Nun wieder Euler:

"§ 115
Da a^ω = 1 + kω ist, so wird, welche Zahl man auch für i setzen möge:
a^iω = (1 + kω)ⁱ. Es ist mithin:

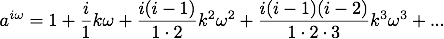
Setzt man nun i = z/ω, wobei z irgend eine endliche Zahl bedeuten soll, so wird i, weil ω eine unendlich kleine Zahl ist, unendlich gross [...]. Substituirt man daher z/i für ω, so erhält man:

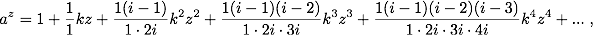
eine Gleichung, die vollkommen richtig ist, sobald für i ein unendlich großer Wert gesetzt wird. k aber ist darin, wie wir sahen, eine bestimmte endliche Zahl, deren Wert von a abhängt."

In §115 wendet Euler den binomischen Satz auf (1 + kω) an, a^iω = (1 + kω)ⁱ. Er geht dabei von irgendeinem Exponenten i aus, den er dann aus vorgegebenen Zahlen z und ω erhält. Von diesem Exponenten wird nicht verlangt, dass er natürlich ist. Dies kann man sich folgendermaßen klarmachen.
Weil z eine beliebige (reelle) finite Zahl sein muss (es soll ja a^z bestimmt werden), kann nicht erwartet werden, dass der Quotient i, i = z/ω, hypernatürlich infinit ist. Die Zahl i liegt aber zwischen zwei benachbarten hypernatürlichen Zahlen, N≤i<N+1. Der Unterschied zwischen N und i ist also höchstens 1 und damit ist iω-Nω≤ω. Die beiden Zahlen z und x, z = iω und x:=Nω, sind also infinitesimal benachbart.
Euler berücksichtigt im nächsten Paragraphen, wie sich die unendliche Größe von i auswirkt:

"§ 116
Da aber i eine unendlich grosse Zahl ist, so wird (i-1)/i = 1 ... . Aus demselben Grunde aber wird (i-2)/i = 1, (i-3)/i = 1 u.s.w. Folglich wird

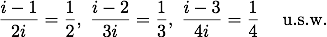
und man erhält daher, wenn man diese Werte einsetzt:

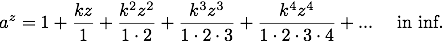
Diese Gleichung giebt aber zugleich die Beziehung an, welche zwischen k und a besteht; denn setzt man z = 1, so wird:

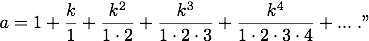
Eulers "Kürzen" geht streng genommen natürlich nicht. Er begründet es mit dem unendlichen Wert von i und verwendet wohlweislich das Wort "wird". Bei Kenntnis finiter und infinitesimaler Zahlen sind aber alle Brüche (i-1)/(2i), (i-2)/(3i), (i-3)/(4i) usw. infinitesimal benachbart zu 1/2 , 1/3 , 1/4 usw.
Offen bleibt aber, ob der Gesamtfehler bei unendlich viele Summanden, bei denen jeder einzelne aus fehlerhaften Faktoren besteht, schließlich infinitesimal bleibt. Euler hat diese Problematik sicherlich durchschaut, aber bei seiner professionellen Erfahrung mit dem Unendlichen war er von der Richtigkeit seiner Überlegung so überzeugt, dass er keine Begründung für nötig erachtete (s. Hinweis am Ende).
Erst in §122 wählt Euler k = 1, da die Basis a beliebig gewählt werden kann, und kommt somit zum Wert seiner Exponentialbasis e.

"§ 122
Da man nun ... die Basis a nach Belieben wählen kann, so kann man sie auch so annehmen, dass k = 1 wird. Setzen wir also k = 1, so erhalten wir [...] :

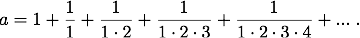
Verwandelt man diese Brüche in Dezimalbrüche und addirt sie sodann, so erhält man für a folgenden Wert:

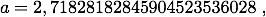
wo auch noch die letzte Ziffer genau ist. [...]

Wir werden nun in der Folge der Kürze wegen für diese Zahl 2,718281828459... stets den Buchstaben e gebrauchen [...] oder es soll e stets die Summe der unendlichen Reihe

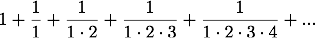
bezeichnen."

Eine ausführlichere Darstellung von Eulers Herleitung, Definition und Eigenschaften der e-Funktion finden Sie in unserem --> Buch zur Nichtstandard-Analysis.