Archimedes von Syrakus (um 287 bis 212 v. Chr.)
Archimedes war der Sohn des Astronomen Pheidias in Syrakus auf Sizilien. Er verkehrte in den höchsten Kreisen seiner Vaterstadt und war sogar mit König Hieron und dessen Sohn und Nachfolger Gelon befreundet. Nur dann und wann - wenn der König ihn bat - verließ er seine rein mathematischen Studien, um "seine Kunst ein wenig vom Abstrakten abzuwenden und auf das Konkrete zu richten und seinen Geist gewöhlichen Menschen zu offenbaren, dadurch, dass er sich in greifbarer Weise mit den Anforderungen der Wirklichkeit beschäftige", so der Geschichtsschreiber Plutarch.Archimedes hat seine Erkenntnisse über den Hebel nicht nur in den Dienst der Verteidigung von Syrakus gegen die vom Meer aus angreifenden Römer unter Marcellus gestellt, sondern auch folgende Episode wird berichtet:
König Hieron hatte das Schiff Syrakosia, ein technisches Wunder, ausgerüstet mit dem raffiniertesten Luxus, als Geschenk für den ägyptischen König Ptolemaios bauen lassen. Wegen seiner außergewöhnlichen Schwere gelang es aber nicht, es ins Wasser zu lassen, bis man Archimedes herbeiholte. Dieser entwarf einen Apparat, den ein einziger Mann ganz allein bedienen konnte. Der König selbst ließ nun das Schiff zu Wasser und rief aus: "Von diesem Tage an soll man Archimedes, wenn er etwas sagt, in allem glauben".
Und Plutarch berichtet weiter: "Obschon diese Erfindungen ihm den Ruhm überirdischer Weisheit eingebracht hatten, wollte Archimedes doch keine Schriften über diese Gegenstände hinterlassen; er fand das Konstruieren von Instrumenten und im allgemeinen jede Tätigkeit, die wegen ihres praktischen Nutzens ausgeübt wird, niedrig und unedel, und er richtete sein Streben nur auf Dinge, die in ihrer Schönheit und Vortrefflichkeit außerhalb von jeglichem Kontakt mit der Nützlichkeit bleiben."
Archimedes stand damit voll auf dem Boden der Platonischen Schule, die das wissenschaftliche Leben des griechischen Altertums bestimmte. Aber genau so, wie er eben doch auch Geräte konstruierte, so benutzte er nebenbei auch Gedanken über das Unendliche, die nach den von Aristoteles beherrschten philosophischen Grundlagen eigentlich nicht statthaft waren.
Er ließ sich aber nicht so leicht in die Karten schauen. Er pflegte nämlich, von Syrakus aus, seine mathematischen Entdeckungen schriftlich seinem Freund, dem alexandrinischen Astronomen Konon auf Samos, mitzuteilen, meistens zuerst ohne Beweis, weil er, wie er selbst in der Einleitung zu der Arbeit über Spiralen schreibt, "gerne jedem Mathematiker das Vergnügen gönnen möchte, es selber zu erfinden". Aber hie und da fügte er auch falsche Lehrsätze hinzu, "damit diejenigen, die behaupten, das alles selber entdeckt zu haben, ohne aber die Beweise hinzuzufügen, auch einmal hereinfallen, indem sie behaupten, etwas gefunden zu haben, das unmöglich ist".
Seine eigenen Beweise aber sind für alle Zeiten mustergültig und enthalten sich gleichzeitig jeden Bezugs auf "verbotene" Gedanken vom Unendlichen. Und das, obwohl er seine Erkenntnisse genau solchen "verbotenen" Ideen verdankte. Nur dadurch ist es ihm als erstem gelungen, krummlinig begrenzte Figuren zu "wiegen", und nur dadurch ist er zum Urvater der Integralrechnung geworden.
Weiter unten wird dargestellt, wie Archimedes mit Hilfe seiner Wiegemethode zum Kugelvolumen gelangte - ein prominentes Beispiel dafür, dass Archimedes' Umgang mit dem "Unendlichen" eine produktive Methode darstellte (im Gegensatz zum heute überwiegend verwendeten Grenzwertformalismus).
Doch zunächst seine eigene Einschätzung dieser Methode:
Archimedes' Einschätzung der Wiegemethode
Einerseits ist Archimedes felsenfest von der Richtigkeit seiner Ergebnisse überzeugt, andererseits muss er sich eingestehen, dass sie mit fragwürdigen Mitteln gewonnen wurden. Denn die wesentlich benutzte Grundidee war doch, dass sich eine Figur aus unendlich vielen Strecken bzw. aus unendlich vielen Kreisen aufbauen lässt. Dem stand jedoch die philosophische Erkenntnis des Aristoteles entgegen: "Es gibt nur endlich viele Dinge." Bis ins 19. Jahrhundert hinein galt weitgehend unangefochten sein Axiom: "Unendliches ist nur der Möglichkeit nach vorhanden", wie es etwa der Prozess des Zählens nahelegt. (Potentiell unendlich im Gegensatz zu aktual unendlich würden wir heute sagen.)Archimedes kannte auch die "Definition" einer Strecke, die nach Euklid zwar eine Länge, aber keine Breite und damit keinen Flächeninhalt besitzt. Und genau so hat ein Kreis zwar einen Flächeninhalt, aber keine Dicke und somit kein Volumen. Wie also soll ein Hebel darauf mechanisch reagieren?
Archimedes hütete sich deshalb, seine Wägemethode zu veröffentlichen, schon gar nicht als wissenschaftliche Publikation. Statt dessen veröffentlichte er seine Entdeckungen mit unangreifbaren Beweisen, in denen er zeigte, dass z.B. die Kugel weder kleiner noch größer als 1/6 des Vergleichszylinders sein könne. Wie er aber auf den Anteil ein Sechstel gekommen war, wusste über die Jahrtausende keiner seiner Nachfahren. Der Mathematiker Wallis drückt seinen Unmut im 16. Jahrhundert, als die Analysis mühsam neu entwickelt werden musste, so aus: "Es ist, als ob Archimedes wie mit Absicht die Spuren seiner Untersuchung verdeckt hätte, als ob er der Nachwelt das Geheimnis seiner Entdeckungsmethode nicht gönnen würde, sie aber doch zwingen wollte, seine Ergebnisse anzuerkennen."
Und doch hatte er seine "Methode" dem jüngeren Mathematiker Eratosthenes mitgeteilt. Nur ist dieses Schriftstück wohl kaum bekannt geworden und dann gänzlich verschollen. Zum Glück waren Abschriften seiner Werke (einschließlich der "Methode") als wertvolles Schreibmaterial ein zweites Mal - diesmal von lateinisch schreibenden Mönchen - beschrieben worden. Diese Schriftrolle wurde erst 1906 gefunden und vom dänischen Philologen Heiberg in Konstantinopel untersucht; er hat die "Methode" noch fast vollständig entziffern können.
Archimedes schreibt darin: "Bei einer früheren Gelegenheit sandte ich Dir einige der von mir gefundenen Lehrsätze, wobei ich nur die Sätze aufschrieb und Dich aufforderte, die vorläufig nicht angegebenen Beweise zu finden. [...] Die Beweise dieser Sätze habe ich also in diesem Buche ausgearbeitet und schicke sie Dir jetzt. [...] habe ich es angebracht gefunden, in demselben Buche eine eigentümliche Methode niederzulegen und Dir auseinanderzusetzen, wodurch es Dir möglich sein wird, eine Anregung zur Untersuchung einiger mathematischer Fragen mithilfe der Mechanik zu gewinnen. Dieses Verfahren ist nach meiner Überzeugung auch für den Beweis der Sätze selbst nicht weniger nützlich, denn gewisse Dinge sind mir zuerst durch eine mechanische Methode klar geworden, mussten aber nachher geometrisch bewiesen werden, weil ihre Behandlung nach der genannten Methode keinen wirklichen Beweis liefert. Denn es ist offenbar leichter, wenn wir durch die Methode einige Kenntnis von den Fragen gewonnen haben, den Beweis zu finden, als ihn ohne vorläufige Kenntnis zu finden."
Das Hebelgesetz
Zwei Körper an einem Hebel halten sich das Gleichgewicht, wenn gilt:Kraft mal Kraftarm = Last mal Lastarm.
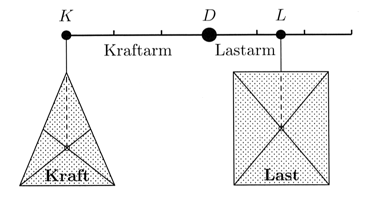
Das ist das archimedische Hebelgesetz. Denkt man sich mit Archimedes Dreieck und Rechteck aus der Abbildung homogen mit Masse belegt, so dass ihr Gewicht dem jeweiligen Flächeninhalt entspricht, so ist hiermit der Satz bildlich dargestellt, dass ein Rechteck den doppelten Flächeninhalt eines (gleichschenkligen) Dreiecks mit gleicher Grundseitenlänge und gleicher Höhe besitzt.
Von ausschlaggebender Bedeutung ist es nun, dass es nur auf die Lage der Punkte K und L relativ zum Drehpunkt D und auf die beiden Gewichte ankommt, aber nicht auf die Gestalt der senkrecht am Hebel angehängten Körper oder die Art ihrer (gewichtslos zu denkenden) Aufhängung. Insbesondere können die Körper auch ohne zusätzliche Aufhängung direkt an die Hebelstange geheftet sein. Wichtig allein ist dabei, dass die "Schwerpunkte" der Körper weiterhin senkrecht unter den Punkten K und L hängen.
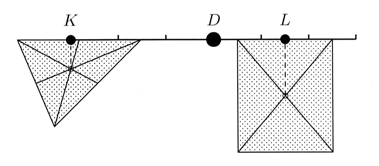
Der Schwerpunkt eines Körpers ist also derjenige Punkt, der den gesamten Körper bei Gleichgewichtsfragen am Hebel vertreten kann, wenn man sich das Gewicht des Körpers in ihm konzentriert denkt. Bei punktsymmetrischen Körpern ist natürlich das Symmetriezentrum der Schwerpunkt - bei anderen wird die viel später entwickelte Methode der Integralrechnung zur Bestimmung herangezogen.
Die Wägung einer Kugel
Besonders stolz war Archimedes darauf, dass es ihm gelungen war, die Kugel zu "wiegen". Dabei folgte er der Grundidee, die Kugel zunächst in parallele Schnittkreise zerlegt zu denken, deren Mittelpunkte, die zusammen einen Kugeldurchmesser bilden, sich als Grundlage für eine Hebelstange anbieten. Ein Maß für das Gewicht eines Kreises ist dann seine Fläche.Und auch ohne Kenntnis der Kreiszahl
 wusste Archimedes, dass deshalb r2 ein
Maß für das Gewicht eines Kreises vom Radius r ist. Befindet sich dieser Kreis im Abstand a
vom Drehpunkt des Hebels entfernt, so ist ein Ausdruck der Form r2·a ein Maß
für seinen Anteil an "Kraft mal Kraftarm". Welcher Körper mit
bereits bekanntem Volumen sich zum Vergleich eignen würde, trat erst während der
Untersuchung eines Schnittkreises bei der Suche nach einem passenden "Kraftarm" zutage (vgl.
folgende Abbildung).
wusste Archimedes, dass deshalb r2 ein
Maß für das Gewicht eines Kreises vom Radius r ist. Befindet sich dieser Kreis im Abstand a
vom Drehpunkt des Hebels entfernt, so ist ein Ausdruck der Form r2·a ein Maß
für seinen Anteil an "Kraft mal Kraftarm". Welcher Körper mit
bereits bekanntem Volumen sich zum Vergleich eignen würde, trat erst während der
Untersuchung eines Schnittkreises bei der Suche nach einem passenden "Kraftarm" zutage (vgl.
folgende Abbildung).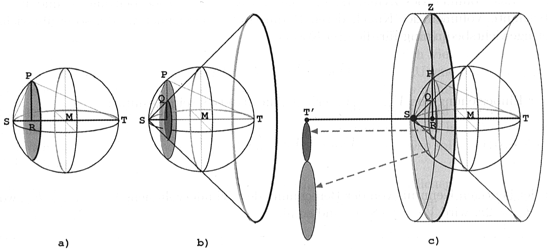
Für jeden Punkt R des Durchmessers ST ergibt sich ein Schnittkreis mit Radius RP und ein rechtwinkliges Dreieck STP im Thaleshalbkreis. Nach dem Höhensatz lässt sich das Quadrat des Schnittkreisradius bestimmen zu
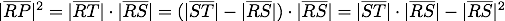
oder
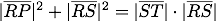 .
.Links stehen Maße für Kreise, es fehlt ein Faktor "Kraftarm". Rechts gibt es kein Gewichtsmaß. Beide Mängel lassen sich durch Multiplikation mit ST beheben:
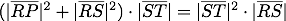 .
.Ein Kreis mit dem Radius RS ergibt für Archimedes keinen Sinn, er ersetzt ihn durch einen Kreis mit demselben Radius RQ, der aber senkrecht zur Achse stehen soll. Die Gesamtheit aller dieser Kreise bildet einen Kegel, dessen Volumen er als ein Drittel des umschließenden Zylinders kennt. Ein brauchbarer Vergleichskörper ist gefunden (Abb. b).
Analog ersetzt er ST durch RZ. Hierdurch kommt ein Vergleichszylinder zusätzlich ins Spiel, dessen Höhe und Radius gleich dem Kugeldurchmesser sind (vgl. Abb. c).
Schließlich sei T' der an S gespiegelte Punkt T. Damit hat Archimedes wieder einen zweiarmigen Hebel; diesmal mit der Gleichgewichtsbedingung von drei Kreisen
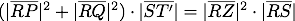 .
.Aus dieser Gleichung ergibt sich, dass der Schnittkreis des Zylinders an der Stelle R, wo er bereits ist, im Gleichgewicht ist zu den beiden Schnittkreisen des Kegels und der Kugel zusammen, wenn sie in T' an die Hebelstange T'T gehängt werden. Weil das für jeden Querschnitt gilt und durch alle Kreise jeweils Zylinder, Kegel und Kugel gebildet werden, sind auch die vollständigen Körper im Gleichgewicht, wenn Kugel und Kegel in T' aufgehängt werden und der Zylinder mit seiner Achse auf der Hebelstange bleibt. Sein Schwerpunkt M ist der Mittelpunkt von ST.
Sei VZ das Volumen des Zylinders, VKe das des Kegels - beide bekannt - und VKu das unbekannte Volumen der Kugel, deren Radius mit r bezeichnet werde, so ergibt sich als Gleichgewichtsbedingung für die drei Körper:
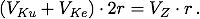
Unter Einbeziehung von VKe = ⅓·VZ erhält Archimedes sein Resultat:
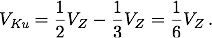
Mit der heutigen Kenntnis von der Berechnung des Zylindervolumens
VZ =
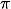 ·(rZ)2·hZ, wobei
rZ = hZ = 2r, wird
VZ =
·(rZ)2·hZ, wobei
rZ = hZ = 2r, wird
VZ = 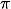 ·8·r3 und somit
·8·r3 und somit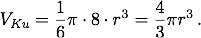
Die Größen des Vergleichszylinders und des -kegels im Verhältnis zur Kugel gefielen Archimedes nicht. "Schön" hingegen ist ein Zylinder, dem Kugel und Kegel einbeschrieben sind. In diesem Fall gilt:
Die Volumina von Kegel, Kugel und Zylinder stehen im Verhältnis 1:2:3. (Warum?)
Der Schnitt durch die drei Körper, der die Zylinderachse enthält, schmückte auf Wunsch des Archimedes seinen Grabstein.
Archimedes' Wägung des Parabelsegments (d.h. Integration der Parabel), seine Beweise dazu und zum Kugelvolumen finden Sie in unserem --> Buch zur Nichtstandard-Analysis.





