Tutorials zur Nichtstandard-Analysis
Standard- und Nichtstandard-Analysis — alt und neu
F: Was soll denn das bedeuten? Gibt es zwei verschiedene Gebiete „Analysis”?A: Nein, natürlich nicht, auch wenn die Überschrift diesen Gedanken nahelegt.
F: Und wieso spricht man von „Standard” und „Nichtstandard”? Hat das etwas mit „normal” und „unnormal” zu tun?
A: Nein, das meint man ebenfalls nicht. Es hat etwas mit der Geschichte der Analysis und mit der Herangehensweise an deren Fragestellungen zu tun. Und dann passen eher Begriffspaare wie „alt – neu” oder „herkömmlich – modern”
F: Erzähl doch mal.
A: Nun denn! Seit etwa dreihundert Jahren beschäftigt man sich intensiv mit Themen wie der Steigung einer Kurve oder dem Inhalt einer Fläche mit krummen Rändern. Da traten nämlich völlig neue Probleme auf.
F: Welche denn?
A: Nehmen wir als Beispiel die Steigung einer Kurve. Was meinst Du, was man darunter verstehen soll?
F: Na, man sieht doch, dass zum Beispiel eine Parabel an verschiedenen Punkten verschieden steil ist. Im Scheitelpunkt ist sie sogar waagerecht — würde ich jedenfalls sagen... .
A: Du merkst, es bleiben Fragen übrig, denn was soll Steigung in einem Punkt bedeuten? Es geht ja darum, die Steigung zu berechnen. Hast Du eine Idee, wie man vorgehen könnte?
F: Mir fällt nur ein, wie man bei einer Geraden die Steigung berechnet. Man nimmt die Koordinaten zweier Punkte und ... — Ah, schon hier scheint ein Problem zu sein. — Wenn ich an einer bestimmten Stelle die Steigung berechnen will, dann habe ich erst einmal nur einen Punkt.
A: Du brauchst aber zwei Punkte. Woher nimmst Du den zweiten?
F: Hmm! ... Mir stehen eigentlich nur auf der Parabel weitere Punkte zur Verfügung.
A: Naja, dann nimm doch einen davon!
F: Aber dann berechne ich doch nicht die richtige Steigung, das sieht man doch. Da mache ich doch einen Fehler.
A: Stimmt! Die Steigung, die Du so berechnest, ist bestimmt nicht die, die Du suchst. Aber Du findest doch bestimmt einen Weg, damit der Fehler zumindest klein ist.
F: Das ist einfach, dann nehme ich als zweiten Punkt einen, der möglichst nahe am ersten liegt.
A: Sehr gut! Aber wie nahe denn?
F: So nahe wie möglich. ... Ah, das nächste Problem. Zusammenfallen dürfen die beiden Punkte natürlich nicht, denn ich berechne die Steigung zwischen zwei Punkten A(x1;y1) und B(x2;y2) als Quotienten
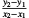 . Hierin darf der Nenner nicht null sein. Aber wenn der Nenner sehr klein ist, dann dürfte der Fehler kaum noch etwas ausmachen. Der Zähler ist dann übrigens auch sehr klein.
. Hierin darf der Nenner nicht null sein. Aber wenn der Nenner sehr klein ist, dann dürfte der Fehler kaum noch etwas ausmachen. Der Zähler ist dann übrigens auch sehr klein.A: Wie klein soll denn der Nenner sein? Oder wie nahe soll der zweite Punkt dem ersten sein?
F: Sagen wir mal, im Nenner kommt als Differenz eine Dezimalzahl wie „Null Komma – unendlich viele Nullen – und dann eine Eins” heraus.
A: Unendlich viele Nullen hinter dem Komma? Und dann eine Eins? Wie meinst Du das?
F: Vielleicht so etwas wie „Periode null”? ... Ach nein, das geht ja nicht. Es wäre keine Periode mehr, wenn dann wieder etwas anderes käme.
A: Genau! Aber halten wir erst einmal fest, was unendlich viele Nullen hinter dem Komma oder „Periode null” bedeutet. Alle ganzen Zahlen in der Menge
 haben diese Eigenschaft. Die aber können wir für die Steigung nicht gebrauchen, auch nicht die Null selbst, wie Du schon erkannt hast. Von „unendlich vielen Nullen” spricht man hier, weil es keine letzte Null gibt. Es sind potentiell unendlich viele Nullen. Wollte man nämlich diese Nullen durchnumerieren, dann hätte jede, der man gerade eine Nummer geben will, eine endliche Nummer. Aber man wird nie fertig. Dieses potentiell unendlich ist das Wesen der natürlichen und auch der reellen Zahlen.
haben diese Eigenschaft. Die aber können wir für die Steigung nicht gebrauchen, auch nicht die Null selbst, wie Du schon erkannt hast. Von „unendlich vielen Nullen” spricht man hier, weil es keine letzte Null gibt. Es sind potentiell unendlich viele Nullen. Wollte man nämlich diese Nullen durchnumerieren, dann hätte jede, der man gerade eine Nummer geben will, eine endliche Nummer. Aber man wird nie fertig. Dieses potentiell unendlich ist das Wesen der natürlichen und auch der reellen Zahlen.Wir sind hier an der Stelle angekommen, wo sich die alte Standardanalysis von der neuen Nichtstandardanalysis unterscheidet. Bei der Nichtstandardanalysis gibt es Zahlen, die hinter dem Komma wirklich unendlich viele Nullen besitzen, bevor eine andere Ziffer kommt. Diese andere Ziffer hätte dann eine „echt unendliche Nummer”. In solch einem Fall spricht man von aktual unendlich.
F: Kannst Du mir das einmal genauer erklären?
A: Das ist erst einmal ganz einfach. Jede reelle Zahl, die man sich konkret vorstellen kann, ist im Endlichen und damit auch jede natürliche Zahl, denn mit denen würde man die Stellen hinter dem Komma abzählen. Also kann eine reelle Dezimalzahl, die keine ganze Zahl ist, nur endlich viele Nullen hinter dem Komma haben, bevor eine andere Ziffer kommt, denn man muss die Dezimalziffern ja abzählen können. Kämen unendlich viele Nullen, dann wäre es die reelle Null bzw. eine andere ganze Zahl.
F: Dann lässt sich ein Fehler bei der Steigungsberechnung ja gar nicht vermeiden.
A: Streng genommen nicht, aber der Fehler muss so klein sein, dass er in der Menge
 keine Bedeutung mehr hat. So einen kleinen Betrag hat aber keine reelle Zahl — außer der Null, aber die darf nicht im Nenner stehen. Zur Berechnung der Steigung braucht man also Zahlen, deren Betrag kleiner ist als jede positive reelle Zahl, aber ungleich null. Solche Zahlen können dann aber nicht mehr reell sein.
keine Bedeutung mehr hat. So einen kleinen Betrag hat aber keine reelle Zahl — außer der Null, aber die darf nicht im Nenner stehen. Zur Berechnung der Steigung braucht man also Zahlen, deren Betrag kleiner ist als jede positive reelle Zahl, aber ungleich null. Solche Zahlen können dann aber nicht mehr reell sein.F: Ich verstehe. Dann ist also der zweite Punkt, den man für die Steigung braucht, so nahe am ersten, dass die Steigung dann zwar noch einen Fehler aufweist, der aber in der Menge der reellen Zahlen keine Bedeutung mehr hat.
A: Richtig! Die berechnete Steigung besteht dann aus einem reellen Teil und einem, wie man sagt, infinitesimalen Teil. Streicht man den infinitesimalen Teil weg, dann hat man tatsächlich die reelle Steigung der Kurve, und zwar in einem Punkt.
F: Das klingt ja einfach.
A: Ist es auch.
F: Und warum hat man das nicht immer so gemacht?
A: Nun, die „Väter der Analysis”, zum Beispiel Leibniz und Newton, rechneten so. Sie nahmen solche infinitesimalen Zahlen einfach als gegeben an und kamen zu ihren richtigen Ergebnissen. Aber es gelang ihnen nicht, diese Zahlen in das Gedankengebäude der Mathematik einzubauen. Das gelang erst Abraham Robinson in den 1960er Jahren.
F: Und bis dahin hat man einfach mit Zahlen gerechnet, die es gar nicht gab?
A: Man hat einen anderen, keineswegs leicht zu verstehenden Weg beschritten, um sicher zu sein, dass die Berechnungen richtig sind. Newton und Leibniz, auch Euler, rechneten zwar richtig, aber beim Rechnen mit infinitesimalen Zahlen sind schon ein paar Regeln zu beachten, um Rechenfehler zu vermeiden. Und die beherrschte nicht jeder. Man war im Laufe der Zeit zunehmend unzufrieden mit dieser Situation.
F: Und wie geht dieser, wie Du sagst, schwierige Weg?
A: Das ist die Standardanalysis, also die herkömmliche Analsysis. Ich versuche einmal, es kurz zu beschreiben. Stell Dir vor, Du lässt den x-Wert des zweiten Punktes auf den des ersten Punktes zulaufen, aber nach einer zahlenmäßigen Gesetzmäßigkeit, so dass Du die Folge dieser Punkte numerieren kannst. Dann wird der Abstand ja immer kleiner. Wenn Du dann einen Restabstand vorgibst, dann kannst Du ausrechnen, ab welcher Nummer, also dem wievielten Punkt, alle weiteren Punkte noch näher am ersten Punkt sind.
F: Das klingt doch gar nicht so schwierig.
A: Ja, dem will ich nicht widersprechen. Aber man muss beweisen, dass das für jeden vorgegebenen Abstand funktioniert ...
F: Naja ...
A: ... und für jede denkbare zahlenmäßige Gesetzmäßigkeit, mit der der zweite Punkt auf den ersten zulaufen kann.
F: Das ist schon viel komplizierter. Wie macht man denn das?
A: Man kann keine konkreten Zahlen verwenden. Bedenke, dass ich in zweierlei Hinsicht das Wort jede benutzt habe. Man muss sich einen abstrakten Prozess vorstellen, der zum richtigen Ergebnis strebt, also zum Abstand null der beiden x-Werte. Man sagt, die Folge der x-Abstände strebt gegen den Grenzwert null.
F: Was heißt denn hier streben?
A: Soviel wie „dass es schon dahin gehen wird”. Etwa so, als wenn man auf seinem Weg an einen unüberwindlichen Zaun kommt, aber genau weiß, dass das Ziel hinterm Horizont erreicht wird, wenn man weiterginge.
F: Ach ja ... ?
A: Hab keine Bedenken, das ist schon einwandfrei, denn man beweist etwas für alle denkbaren Folgen, also Wege, und für alle denkbaren Zäune, an die man unterwegs kommen könnte.
F: Und was ist mit der Steigung?
A: Mit dieser einen Folge der x-Abstände strebt die Folge der zugehörigen Steigungen gegen die Kurvensteigung. Das lateinische Wort für Grenzwert ist übrigens Limes. Aber wohlgemerkt: Jede konkrete Zahleneinsetzung würde zeigen, dass ein nicht tolerierbarer Fehler vorhanden ist.
F: Oje! ... Und die Nichtstandardanalysis?
A: Das haben wir im Grunde schon besprochen. Seit Robinson bewiesen hat, dass man den Körper der reellen Zahlen um unendliche Zahlen erweitern kann und dabei die Rechengesetze und die Ordnungsrelation erhalten bleiben, braucht man nur mit Hilfe dieser Zahlen die Steigung auszurechnen. Man nimmt als Differenz x2-x1 eine Zahl, mit der man von vornherein die Vorstellung infinitesimal, also unendlich kleiner Betrag, verbindet. Als Du vorhin an „Eins Komma – unendlich viele Nullen – und dann eine Eins” dachtest, hast Du Dir offenbar solch eine infinitesimale Zahl vorgestellt. Man rechnet dann die Steigung aus, die natürlich noch einen infinitesimalen Fehler aufweist, und nimmt vom Ergebnis den reellen Teil. Fertig!
F: Dann sollte man doch dieses Verfahren Standard nennen.
A: Das sehe ich im Grunde auch so. Aber in der Wissenschaft, die ja zu recht bei neuen Methoden zunächst kritisch ist, dauert es häufig längere Zeit, bis etwas Neues Allgemeingut wird.






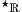 – Teil 1
– Teil 1