Gibt es „Lücken” auf der Zahlengeraden?

F: Als wir in der Schule die irrationalen Zahlen kennengelernt hatten, sagte meine Mathematiklehrerin, auf der Zahlengeraden würden sie die Lücken zwischen den rationalen Zahlen schließen. Das habe ich nie so richtig verstanden, denn wenn es vorher Lücken gab, dann hätten wir die rationale Zahlengerade nie durchzeichnen dürfen. Und bei der reellen Zahlengerade fehlen ja die hyperreellen Zahlen. Dann hätte man die reelle Zahlengerade auch nie durchzeichnen dürfen. Ist das richtig?
A: Nein, alle diese Zahlengeraden zeichnet muss durch. Es ist vielleicht etwas unvorsichtig, von Lücken auf einer Zahlengeraden zu sprechen, wenn man mit einem neuen Verfahren neue Zahlen findet.
F: Das musst Du mir erklären.
A: Zunächst halten wir fest, dass die Zahlengerade immer eine Veranschaulichung einer Zahlenmenge ist, auf der man die Anordnung der Zahlen gut sichtbar machen kann. Auf keinen Fall „ist” die Gerade eine Zahlenmenge.
Aber nun zu unserem Thema. Die rationalen Zahlen liegen, wie man sagt, „dicht”. Das kann man sich ganz einfach klarmachen. Wenn Du mir zwei rationale Zahlen nennst, wird es mir immer gelingen, eine Zahl dazwischen anzugeben. Und nicht nur das. Ich könnte sogar beliebig viele Zahlen angeben, die zwischen Deinen beiden Zahlen liegen. Sag mir mal zwei rationale Zahlen ...
F: Nicht nötig, das ist doch wirklich einfach. Zwischen 15,245 und 15,246 liegen 15,2453 und 15,245627 und noch unendlich viele andere rationale Zahlen. Und mit Brüchen gelingt mir das auch. Zwischen 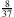und 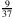liegen zum Beispiel 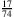, , 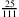, 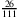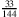und so weiter und so fort.
A: Du siehst also ein, dass man die Zahlengerade als durchgezogene Linie zeichnen muss, auch wenn sie „nur” die Menge 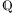veranschaulicht.
Man bezeichnet übrigens die Menge der rationalen Zahlen als abgeschlossen.
F: Wieso? Was bedeutet das?
A: Ich muss es etwas genauer sagen: Abgeschlossen bezüglich der Grundrechenarten. Damit ist gemeint, dass man immer innerhalb der Menge 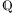der rationalen Zahlen bleibt, wenn man mit ihnen addiert oder multipliziert. Bei dem Wort abgeschlosen könnte man denken, es gäbe keine weiteren Zahlen mehr.
F: Aber wieso spricht man davon, liege in einer Lücke zwischen zwei rationalen Zahlen. Könnte man denn die rationalen Nachbarzahlen angeben?
A: Nein, in dieser Einfachheit nicht, denn die rationalen Zahlen sind nicht in Form einer Perlenschnur aneinandergereiht, wie man es von den natürlichen und den ganzen Zahlen her kennt. Und folglich ist es auch mit den „Zwischenräumen” nicht so einfach. Gleichwohl kann man die rationalen Zahlen mit dem Cantorschen Diagonalverfahren in eine Reihenfolge bringen und somit abzählen. Dann sind sie aber nicht der Größe nach geordnet. Ich denke, wir sollten uns noch einmal klarmachen, wie man die rationalen und später die irrationalen Zahlen gewinnt.
F: Wollen wir mit der natürlichen Zahlengeraden anfangen?
A: Hier zeichnet man keine Gerade, sondern einen Strahl, denn es gibt einen Anfang. Der Strahl ist aber auch nur ein Modell. In gleichen Abständen markiert man die einzelnen natürlichen Zahlen wie Perlen auf einer Schnur. Jede hat ihren Nachfolger und, bis auf die Anfangszahl Null, einen Vorgänger.
F: Ok, ich war ungenau. Dass hier keine Zahlengerade vorliegt, weiß ich ja. Aber wenn ich die negativen Zahlen hinzunehme, liegen diese doch auf einer Geraden.
A: Ja, aber immer noch wie Perlen auf einer Schnur. Erst mit der Einführung der Bruchzahlen bekommen auch die Zwischenräume eine Bedeutung, nämlich dass auch der gesamte Bereich zwischen den ganzen Zahlen gefüllt ist, und zwar mit Bruchzahlen. Diese rationale Zahlengerade enthält übrigens ausschließlich Bruchzahlen. Aus diesem Grunde muss man sich auch die ganzen Zahlen als Brüche mit dem Nenner eins vorstellen, also zum Beispiel 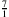oder .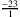
F: Warum das?
A: Weil die rationalen Zahlen eine neue Zahlenmenge bilden, in die die ursprünglichen ganzen Zahlen eingebettet werden. Die rationalen Zahlen sollen das Ergebnis der Division „Zähler durch Nenner” sein, weswegen man die ursprüngliche Divisionsaufgabe in der besonderen Form eines Bruches hinschreibt: 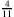soll das Ergebnis der Division 4:11 sein.
F: So einfach?
A: Ja, so einfach. Und weil innerhalb der Menge der rationalen Zahlen die Rechengesetze gelten, bilden sie algebraisch einen Körper.
F: Was meint man damit?
A: Nun, es gibt zwei Rechenarten, Addition und Multiplikation. Für beide Rechenarten gilt ein Kommutativ- und ein Assoziativgesetz, zu jeder Rechenart gehört eine neutrale Zahl, 0 bzw. 1, und beide Rechenarten sind über das Distributivgesetz miteinander verbunden. Und schließlich besitzt jede Zahl bezüglich der Addition ihre Gegenzahl und bezüglich der Multiplikation, bis auf die Null, ihre Kehrzahl. Wenn eine Zahlenmenge diese Eigenschaften aufweist. spricht man von einem Zahlenkörper.
F: Was ist mit Subtraktion und Division?
A: Die braucht man eigentlich nicht mehr.
F: Wieso?
A: Man kann jede Subtraktion ersetzen, indem man stattdessen die Gegenzahl des Subtrahenden addiert, also statt 9 − 5 rechnet man 9 + (−5). Und jede Division kann man durch die Multiplikation mit der Kehrzahl des Divisors ersetzen, also statt 14 : 3 rechnet man 14 ⋅ 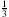. Man kann diese beiden Rechenarten abschaffen, aber im Alltag benutzt man sie trotzdem. Übrigens gibt es bei Subtraktion und Division kein Kommutativ- und kein Assoziativgesetz. Indem man sie durch Addition und Multiplikation ersetzt, gelten diese Gesetze umfassend.
Kommen wir wieder zurück zum Zahlenkörper. Es kommt noch weiteres Neues hinzu, was es bei den ganzen Zahlen nicht gab, denn es gibt Brüche, die dieselbe Zahl bedeuten.
F: Ja, ich weiß. Die Brüche 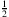, 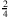und 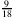sind verschiedene Schreibweisen für dieselbe rationale Zahl. Genauso stehen 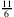, 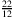und 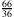für dieselbe, aber eine andere, Zahl.
A: Man sagt, dass alle Brüche, die ein und dieselbe Zahl beschreiben, jeweils eine Äquivalenzklasse bilden. Im Grunde sind es verschiedene Schreibweisen für dieselbe rationale Zahl.
F: Dass zwei Brüche dieselbe Zahl beschreiben, würde man sofort merken, wenn man die Divisionen Zähler durch Nenner ausführt. Man erhält 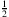= = 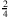= 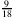0,5
bzw. 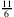= = 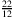= 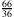1,83.
A: Wie heißt Dein letztes Ergebnis?
F: Eins Komma acht Periode drei.
A: Du hast es richtig gesprochen. Das Wort „Periode” sagt man, wenn sie beginnt, nicht wenn sie endet. Und hier sind wir bei einer weiteren Eigenschaft der rationalen Zahlen, die sogar ihr Kennzeichen ist. Jede rationale Zahl besitzt in Dezimalschreibweise eine Periode.
F: Ist dann von 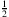die Dezimalschreibweise null Komma fünf Periode null, also 0,50?
A: Völlig richtig! Es geht sogar noch weiter, denn jede ganze Zahl hat dann eine Periode null, zum Beispiel −35,0. Wie gesagt, an ihrer periodischen Dezimalschreibweise erkennt man immer, dass man eine rationale Zahl vor sich hat. Allerdings gebe ich zu, dass dies Nichtmathematikern ein wenig künstlich anmutet.
F: Wie kommt es eigentlich zu den Perioden?
A: Man verwandelt einen Bruch in eine Dezimalzahl, indem man die Division ausführt. Geht die Division nicht auf, dann bleibt immer ein Rest. Hat man zum Beispiel einen Siebentelbruch, dann kann es aber nur sechs verschiedene Reste geben. Tritt nun ein Rest zum zweiten Mal auf, dann ist die Periode da. Ein Siebentelbruch hat tatsächlich eine sechsstellige Periode, ein Sechstelbruch dagegen, wie Du gesehen hast, nur eine einstellige. Die Regel ist, dass eine Division durch n eine höchstens (n−1)-stellige Periode ergeben kann.
F: Und wenn die Division aufgeht, ist also immer eine Periode null anzufügen.
A: Genau! Zumindest denken sollte man sie sich. Mit „Periode null” würde man deutlich machen, dass die ganze Zahl 2 in die Menge der rationalen Zahlen eingebettet wurde.
F: Kommen wir doch nun zu den irrationalen Zahlen. Die sollen zwischen den rationalen Zahlen liegen. Und als Dezimalzahlen enden sie hinter dem Komma nie, aber eine Periode tritt auch nicht auf. Wie ist denn das zu erklären?
A: Zunächst betone ich noch einmal, dass auf der rationalen Zahlengeraden keine Lücken sind. Und trotzdem ist etwas an Deiner Beschreibung richtig. Weißt Du noch, wie man herausfindet, dass zum Beispiel nicht rational sein kann?
F: Ja, man sucht die Stelle, an der auf der Zahlengeraden liegt. Weil ()² gleich 2 ist, sucht man zwischen 1 und 2, denn 1² = 1 und 2² = 4. Mit 1,5 ist man immer noch zu weit rechts, denn 1,5² = 2,25. Mit 1,4 erhält man 1,4² = 1,96 und ist schon ziemlich nahe dran. So probiert man immer weiter, man nennt das eine Intervallschachtelung. bis man mit dem Taschenrechner ...
A: Was macht der Taschenrechner?
F: Na, wenn man die Wurzeltaste drückt, erhät man ... Moment mal! ... Man erhält 1,414213562. Wenn ich damit nun die Quadrattaste drücke, steht auf dem Taschenrechner 2, dann habe ich es doch.
A: Oh nein! Wenn du das glaubst, dann bist Du auf Deinen Taschenrechner hereingefallen.
F: Wieso?
A: Stell Dir einmal vor, das Quadrat schriftlich auszurechnen, also
1,414213562 ⋅ 1,414213562.
Dann würdest Du Zeile für Zeile multiplizieren, immer um eine Stelle versetzt, und dann addieren. Weil bei den beiden Faktoren jeweils 9 Stellen hinter dem Komma sind, erhält das Produkt 18 Stellen hinter dem Komma. Und da glaubst Du, dort stehen nur Nullen? Ich erkenne doch jetzt schon, dass die allerletzte Stelle eine 4 ist.
F: ...?
A: Schreiben wir doch einmal den Aufbau solch einer schriftlichen Multiplikation hin:

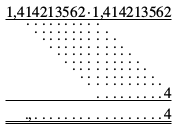
F: Ach so! In der letzten Zeile steht das Produkt 1,414213562 ⋅ 2, und zwar am weitesten nach rechts versetzt. Und dort steht ganz rechts 4, weil 2 ⋅ 2 gleich 4 ist. Also hat mich doch der Taschenrechner angeschwindelt.
A: Zumindest sollte man sich nicht blindlings auf ihn verlassen. Aber gehen wir noch einen Schritt weiter, denn vielleicht hat der Taschenrechner nicht genügend Stellen hinter dem Komma anzeigen können. Welche Ziffer müsste denn als letzte Dezimalstelle für stehen, damit im Quadrat am Ende eine Null steht?
F: Endet die Anzeige mit 1, dann endet das Quadrat ebenfalls mit 1, denn 1 ⋅ 1 = 1, die 2 hatten wir schon, 3 ⋅ 3 = 9, 4 ⋅ 4 = 16, also eine 6 am Ende. ... Bei 5 steht eine 5 am Ende, geht also nicht, bei 6 eine 6, ... . Da geht ja gar nichts. ... Doch, weil 0 ⋅ 0 = 0 ist, geht es mit der 0.
A: Das hilft Dir aber gar nicht, denn wenn an der letzten Stelle 0 steht, hast Du dasselbe Problem an der vorletzten Stelle. Dort müsste dann auch eine 0 stehen und so weiter. Man kann also gar nicht fertig werden. Und das Verfahren der Intervallschachtelung lässt gar nicht erkennen, wann eine Periode entstehen kann. Zwar kann sich eine Ziffernfolge irgendwo ein paarmal wiederholen, aber das wäre keine Periode.
F: Dann ist mir klar, dass keine rationale Zahl sein kann. Also gibt es doch eine Lücke?
A: Nein, denn wir haben mit einem anderen Verfahren, nämlich der Intervallschachtelung, gefunden, nicht mehr mit den Grundrechenarten. Deshalb spricht man nun von irrationalen Zahlen. Und ich will Dir sagen, dass man mit dem Verfahren Intervallschachtelung auch die rationalen Zahlen findet. Damit sind sie eingebettet in diese Menge, die man nun die Menge der reellen Zahlen nennt. Sie ist wesentlich größer als die Menge der rationalen Zahlen.
F: Gibt es auch hier wieder eine Äquivalenzrelation, die dann mehrere Intervallschachtelungen zu einer reellen Zahl zusammenfasst?
A: Ja, natürlich! Unsere Intervallschachtelung für waren bereits zwei Zahlenfolgen. Alle linken Ränder bzw. alle rechten Ränder bilden jeweils eine konvergente Folge, die, wie man sagt, dem Grenzwert zustrebt. Und es gibt viele weitere Folgen mit diesem Grenzwert. Ganz entsprechend gibt es viele konvergente Zahlenfolgen mit anderen rationalen oder irrationalen Zahlen als Grenzwert. Und noch etwas: Auch wenn man irrationale Zahlen als Folgenglieder zulässt, ergibt das Verfahren der Intervallschachtelung immer nur reelle Zahlen. Erinnere Dich daran, dass wir die Stelle, wo auf der Zahlengeraden liegt, zunächst nur mit rationalen Zahlen eingeschachtelt haben.
Man sagt übrigens, die Menge 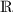der reellen Zahlen sei vollständig, vergisst aber häufig den Zusatz bezüglich der Intervallschachtelung oder bezüglich der Grenzwertbildung. Vielleicht denken viele wegen dieses Begriffes vollständig, dass man keine zusätzlichen Zahlen mehr finden könnte.
F: Dann gibt es also auch zwischen den reellen Zahlen bei diesem Verfahren keine Lücken auf der Zahlengeraden, aber mit einem anderen Verfahren könnte man durchaus wieder neue Zahlen finden, die nicht reell sind, aber zwischen reellen Zahlen liegen. Dann müsste man wieder zeigen, dass man mit dem neuen Verfahren auch die reellen Zahlen finden kann, womit sie dann einbettet sind.
A: Ja, und so findet man die hyperreellen Zahlen. Und auch hier ist die Zahlengerade das Modell, mit dem man die hyperreellen Zahlen und ihre Anordnung veranschaulicht. Das Verfahren ist zunächst, dass man sämtliche reellen Folgen, nicht nur die konvergenten, zur Beschreibung von Zahlen erlaubt. Mit den konstanten Folgen sind dann die reellen Zahlen eingebettet. Die neue Äquivalenzrelation heißt genügend viel, womit ausgedrückt wird, dass zwei Folgen dieselbe hyperreelle Zahl beschreiben, wenn sie in genügend vielen Folgengliedern übereinstimmen. Zum Thema „Genügend viel” unterhalten wir uns in einem eigenen Tutorial.
F: Und was beschreiben die konvergenten Folgen bei dieser Äquivalenzrelation?
A: Hier beschreiben sie zumeist hyperreelle Zahlen, die nicht gleichzeitig reell sind, sondern zu einer reellen Zahl infinitesimal benachbart sind.
F: Ach so! Die konstanten Folgen sind zwar auch konvergent, aber es gibt konvergente Folgen, die nicht konstant sind, wie wir bei den Intervallschachtelungen gesehen haben. Also hat man tatsächlich zusätzliche Zahlen gefunden.