„Genügend viel”, „Genügend oft” — Was meint man damit? — Teil 2

F: Wir haben im ersten Teil darüber gesprochen, wann zwei Zahlenfolgen dieselbe hyperreelle Zahl beschreiben. Völlig klar war, dass zwei Folgen, die sich nur bei endlich vielen Indizes unterscheiden, dieselbe Zahl bedeuten. Endlich viele Unterschiede sind nicht genügend viel.
A: Man sagt, dass fast alle Folgenglieder übereinstimmen. Fast alle bedeutet alle bis auf endlich viele. Wir hatten aber auch festgestellt, dass unendlich viele Folgenglieder nicht genügend viel sein können.
F: Darauf kamen wir anhand der Folgen, die sich im Zweier- oder im Dreierrhythmus mit Nullen und Einsen abwechselten. Dann konnte man bei den Folgen im Zweierrhythmus selbst festlegen, dass zum Beispiel nur die Folgenglieder mit geraden Indizes genügend viele sind. Alle ungeraden, von denen es unendlich viele gibt, sind dann nicht genügend viele.
A: So ist es! Man ist aber völlig frei, auch die Menge der ungeraden Indizes als genügend viel festzulegen.
F: Und bei den Folgen im Dreierrhythmus hatte man ebenfalls die Freiheit, zum Beispiel alle durch drei teilbaren Indizes als genügend viel zu erklären. Verbindet man beide Festlegungen miteinander, so reichen sogar alle durch sechs teilbaren Indizes aus, um zu entscheiden, ob zwei Zahlenfolgen dieselbe hyperreelle Zahl beschreiben. Wichtig ist es, zu verstehen, dass man zwar immer unendlich viele Folgenglieder für unbedeutend erklärt, aber auch immer unendlich viele als bedeutend übrigbleiben. Man hat also, obwohl man unendlich viele Folgenglieder aussortiert hat, immer noch genauso viele wichtige Folgenglieder wie vorher. Das liegt daran, dass man die Erkenntnisse aus dem Endlichen – wenn ich etwas wegnehme, dann habe ich danach weniger – nicht ohne weiteres ins Unendliche übernehmen kann. Gibt es denn auch Fälle, in denen man aus einer unendlichen Menge unendlich viele Elemente wegnimmt, aber danach weniger hat?
A: Ja, das ist sogar ganz einfach. Stell Dir vor, Du nimmst aus der Menge 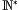alle Zahlen weg, die größer als 100 sind. Dann bleiben 100 Elemente übrig, und das sind weniger als unendlich viele.
F: Ach so! Na klar!
A: Wir wollen von nun an nicht mehr die Folgen selbst betrachten, sondern nur noch von ihren Indizes sprechen.
F: Meinst Du die Indizes, bei denen Zahlenfolgen übereinstimmen müssen, wenn sie dieselbe hyperreelle Zahl beschreiben?
A: Richtig! Unser beispielhaftes Vorgehen mit Folgen im Zweier- und im Dreierrhythmus hat uns zunächst dahin geführt, nur noch die Indizes 6, 12, 18, 24, 30 usw. betrachten zu müssen...
F: Wären bei anderem Vorgehen nur noch die Indizes 5, 11, 17, 23, 29 usw. zu betrachten gewesen?
A: Genau! Wir hätten auch bei den Indizes 4, 10, 16, 22, 28 usw. ankommen können. Aber da noch längst nicht alle Zahlenfolgen verarbeitet waren, bedeutet das, dass für die Relation genügend viel noch viele dieser Indizes zu unbeachtlichen werden.
F: Ok! und wenn ich es richtig verstanden habe, geht es nicht darum, eine ganz bestimmte endgültige Indexmenge zu finden, sondern nur darum, ob man bei irgendeiner letzten Indexmenge ankommt, wenn alle denkbaren Zahlenfolgen verarbeitet sind.
A: Jawohl! Es ist wichtig, dass Du Dir nun im Klaren darüber bist, worum es im Grunde geht. Also fangen wir an.
F: Ja, nun mach schon!
A: Wenn wir von der Indexmenge 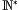sprechen, so denken wir daran, dass zwei Folgen völlig gleich sind, also Glied für Glied übereinstimmen.
F: Dann ist natürlich dieselbe Zahl gemeint.
A: Es reicht aber aus, wenn zwei Folgen nur in fast allen Gliedern übereinstimmen, um dieselbe Zahl zu beschreiben. Dann ist diese Indexmenge nur eine Teilmenge von .
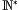F: Also ist jede Teilmenge von 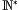, die fast alle natürlichen Zahlen enthält, genügend viel.
A: Richtig! Aber es gibt auch Teilmengen von 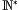, bei denen unendlich viele natürliche Zahlen „fehlen”.
F: Ja, zum Beispiel die Menge aller geraden Zahlen, denn die unendlich vielen ungeraden Zahlen sind nicht drin.
A: Richtig, aber bleiben wir zunächst bei allen Teilmengen, die fast alle natürlichen Zahlen enthalten. Sie sind geeignet, enthalten also genügend viele Elemente. Das bedeutet für zwei Folgen, die bei fast allen Indizes übereinstimmen, dass sie dieselbe Zahl beschreiben.
F: Solche Beispiele hatten wir doch!
A: Ja, so beschreibt die Folge
(2 ; 2 ; 5 ; 5 ; 5 ; 5 ; 5 ; 5 ; ...) die Zahl 5, und die zugehörige Indexmenge ist
I₁ = {3 ; 4 ; 5 ; 6 ; 7 ; 8 ; ...}. Beachte die verschiedenen Klammerarten! Bei runden Klammern meint man Folgen, bei geschweiften Klammern meint man Mengen.
F: Und die Folge
(7 ; 7 ; 7 ; 2 ; 2 ; 2 ; 7 ; 7 ; ...) beschreibt die 7. Dazu gehört die Indexmenge
I₂ = {1 ; 2 ; 3 ; 7 ; 8 ; ...}.
A: Wir halten fest: Stimmen zwei Folgen bei der Indexmenge I₁ oder bei der Indexmenge I₂ überein, dann beschreiben sie dieselbe Zahl. Das ist aber noch nicht alles. Der Durchschnitt beider Indexmengen reicht ebenfalls aus, um dieselbe Zahl zu beschreiben.
F: Der Durchschnitt sind die Indizes, die sowohl in I₁ als auch in I₂ vorkommen, das ist die Indexmenge
I₁ ∩ I₂ = {3 ; 7 ; 8 ; ...}. Das sind immer fast alle natürlichen Zahlen.
A: Und jede Obermenge dieser beiden Indexmengen gehört ebenfalls dazu.
F: Das sind die Mengen, für die I₁ und I₂ Teilmengen sind, also zum Beispiel
{2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; ...},
{1 ; 2 ; 3 ; 6 ; 7 ; 8 ; ...} oder ganz .
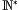A: Nun stell Dir vor, Du würdest aus allen denkbaren Teilmengen von 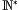alle die herausnehmen, die aus fast allen natürlichen Zahlen bestehen. Das ist so, als würdest Du alle denkbaren Teilmengen von 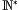durch einen Filter gießen, und in diesem Filter würden die mit fast allen natürlichen Zahlen „hängenbleiben”.
F: Ja, das kann ich mir vorstellen. Und ganz 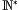ist als eine besondere Teilmenge natürlich auch dabei.
A: In der Mathematik spricht man tatsächlich von einem Filter, und dies sei unser Ausgangsfilter 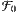. Es geht nun darum, ob es einen umfangreicheren Filter gibt, in dem auch die Indexmenge „hängenbleibt”, die zum Beispiel nur die geraden Indizes enthält, aber auch die entsprechenden Obermengen und alle Schnittmengen, die sich mit den bereits im Filter 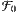vorhandenen bilden lassen.
F: Ich denke, das geht, denn wenn alle geraden Indizes genügend viele sind, dann sind es auch genügend viele, wenn weitere Indizes dazukommen. Wenn also Folgen nicht nur in allen geraden Indizes, sondern auch in weiteren Indizes übereinstimmen, dann sind das auch genügend viel. Die Obermengen würden also auch im Filter „hängenbleiben”.
A: Und was denkst Du, wie die Schnittmenge aus der Menge aller geraden Indizes mit einer Menge aus fast allen Indizes ausssieht?
F: Die würde fast alle geraden Indizes enthalten. Ich denke, das sind dann auch noch genügend viele.
A: Du hast recht. Also können wir den Filter 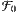zum umfangreicheren Filter 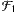erweitern, denn die Menge aller geraden Indizes haben wir soeben zu genügend viel erklären können. Viel wichtiger ist aber, dass damit die unendlich große Menge aller ungeraden Indizes tatsächlich als nicht genügend viel bezeichnet werden kann. Sie bleibt nicht im Filter 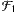„hängen”.
F: Ich vermute, nun kann man den Filter 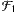zu einem noch größeren Filter 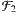erweitern, worin zum Beispiel die Indexmenge mit allen durch drei teilbaren Indizes „hängenbleibt”. Hinzu kommen natürlich auch ihre Obermengen und die Schnittmengen mit allen Indexmengen im Filter .
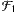A: Sag ruhig, wie die beschaffen sind!
F: Wenn die Obermengen hinzukommen, würde das ja bedeuten, dass zwei Folgen nicht nur dann dieselbe Zahl beschreiben, wenn sie bei allen durch drei teilbaren Indizes übereinstimmen, sondern auch noch bei weiteren Indizes. Klar, das sind dann ebenfalls genügend viele.
A: Und die Schnittmengen?
F: Beim Schnitt mit den Mengen aus fast allen natürlichen Zahlen ist es wie beim Filter 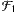. Ein paar, also endlich viele, durch drei teilbare Indizes mit fehlender Übereinstimmung lassen immer noch genügend viele übrig. Und der Schnitt mit der Menge aller geraden Indizes ergibt die Menge aller durch sechs teilbaren Indizes. Das sind unendlich viele und damit auch genügend viel.
A: Du merkst also, dass es funktioniert. Nun erweitert man den Filter 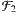zu einem Filter 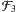, in dem dann weitere unendliche Indexmengen einschließlich Ober- und Schnittmengen „hängenbleiben” und so fort, bis man alle denkbaren Paare von Indexmengen verarbeitet hat, von denen der eine Partner genügend viele und der andere Partner nicht genügend viele Indizes enthält, einschließlich zugehöriger Schnitt- und Obermengen. Dann hätte man einen „ultimativen Eweiterungsfilter” 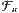, der nicht mehr erweiterungsfähig ist.
F: Das verstehe ich schon, aber was wäre denn gewesen, wenn wir den Ausgangsfilter 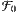anders erweitert hätten, nämlich so, dass die Indexmenge mit allen ungeraden Indizes einschließlich Ober- und Schnittmengen „hängengeblieben” wären?
A: Das wäre ein anderer Erweiterungsfilter gewesen, nennen wir ihn 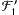. Auf diese Weise wäre eine andere Filterkette entstanden. Statt
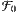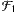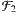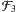⊂ ⊂ ⊂ ⊂ ... hätten wir dann
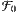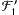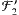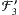⊂ ⊂ ⊂ ⊂ ... erhalten. Auch auf diese Weise wäre man, wenn alle denkbaren Indexmengen verarbeitet worden sind, bei einem „ultimativen Erweiterungsfilter” angekommen, wenn auch bei einem anderen, nennen wir ihn .
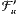F: Mir fällt gerade auf, dass ein Filter offenbar eine Menge ist, die aus lauter Mengen besteht, also eine Menge von Indexmengen. Ist das richtig?
A: Ja, so ist es. Diese Filter lassen sich, wie Du gesehen hast, der Größe nach zu Filterketten ordnen. Allerdings, auch das hast Du erkannt, nicht zu einer einzigen Kette, sondern es gibt nebeneinander viele mögliche Ketten. Deshalb spricht man davon, dass die Menge aller Filter teilweise geordnet ist.
F: Die „Menge aller Filter”? Jeder einzelne Filter ist doch schon eine Menge, deren Elemente Indexmengen sind. Ganz schön kompliziert, sozusagen eine dritte Dimension ...
A: Ja, das muss man sich klarmachen. Alle Indexmengen bestehen aus Zahlen, viele Indexmengen bilden einen Filter, und alle Filter kann man natürlich auch wieder zu einer Menge zusammenfassen. „Noch höher hinaus” gehen wir aber nicht.
F: Na gut! Aber ich habe Dich doch richtig verstanden, dass man über jede Filterkette bei einem „ultimativen Erweiterungsfilter” ankommt. Und je nach Filterkette ist dieser „ultimative Erweiterungsfilter” ein anderer, aber er enthält alle Indexmengen, die für den Vergleich zweier Folgen genügend viel bedeuten. Stimmen die Folgen bei den betreffenden Indizes überein, dann beschreiben sie dieselbe hyperreelle Zahl.
A: Ja, das ist richtig. Soweit also unsere Überlegung.
F: Und kann man das nun beweisen?
A: Leider nicht in Form einer reinen Schlussfolgerung.
F: Wieso sagst Du „leider”? Unsere Idee, nach der Verarbeitung aller Indexmengen bei einem ultimativen Filter anzukommen, klingt doch plausibel.
A: Das Unendliche erweist sich hier als Problem. Weil die Menge 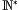potentiell unendlich groß ist, sind auch unendlich viele Paare von Indexmengen zu verarbeiten. Deswegen entstehen auch unendlich lange Filterketten, und von keiner Filterkette kann man folglich ihr letztes Glied angeben.
F: Und wie löst man dieses Problem?
A: Man kann auf jeden Fall sagen, dass die Vereinigung aller Filter wiederum ein Erweiterungsfilter von 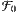ist.
F: Und das reicht nicht?
A: Nein, denn wir können nicht sicher sein, ob wir auf diese Weise Paare von Indexmengen ausgelassen haben, die in keine Filterkette hineinpassen.
F: Kann den das passieren?
A: Ja, das ist teoretisch möglich. Ich will es noch etwas präzisieren. Wir haben immer Paare von Indexmengen verarbeitet und damit die Filter immer umfangreicher gemacht. Von diesen Paaren sollte immer der eine Partner genügend viel bedeuten und der andere Partner, nämlich dessen Komplementärmenge bezüglich 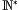, dann immer ungenügend viele Indizes umfassen.
F: Ja, so wie bei einerseits geraden Indizes und andererseits ungeraden Indizes.
A: Aber man kann nicht zweifelsfrei ausschließen, dass es irgendwelche Paare von Indexmengen gibt, die man nicht in genügend viel und ungenügend viel einteilen kann. Es ist denkbar, dass beide Partner ungenügend viele Indizes enthalten. Dann gäbe es keinen ultimativen, also endgültigen, Erweiterungsfilter, denn man hat nicht alle Indexmengenpaare ordnungsgemäß aufteilen können in genügend viel und nicht genügend viel. Es gibt nur den Ausweg, das Auswahlaxiom zu benutzen. Man kennt es auch unter der Bezeichnung Zornsches Lemma. Es besagt, dass es in jeder Filterkette einen „ultimativen Filter” gibt.
F: Bleiben also doch noch Zweifel, ob man den Körper der reellen Zahlen zu den hyperreellen Zahlen erweitern kann?
A: Nein, es gibt keinen Zweifel. Wir haben in diesem Tutorial einen Weg beschritten, wie man die hyperreellen Zahlen aus den reellen konstruieren kann. Und dieser Weg kommt, bisher jedenfalls, nicht ohne das Auswahlaxiom aus. Abraham Robinson hat aber auf einem völlig anderen Weg, nämlich mit den Mitteln der Prädikatenlogik, bewiesen, dass diese Erweiterung möglich ist.
F: Und somit können wir also Analysis mit hyperreellen Zahlen betreiben und den Grenzwert „ad acta legen”.
A: So ist es. Und damit wird das Lernen der Differential- und Intergralrechnung viel leichter.