Tutorials zur Nichtstandard-Analysis
Rechnen in  (bzw.
(bzw. 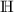 ) — Teil 1
) — Teil 1
F: Wie rechnet man mit hyperreellen Zahlen? Die Rechengesetze der reellen Zahlen gelten auch bei den hyperreellen Zahlen weiter.A: Das müssen sie auch, denn sonst wäre
 keine Erweiterung des reellen Zahlenkörpers. Wichtig ist, dass man mit den hyperreellen
Zahlen tatsächlich im Unendlichen rechnen kann. Dies leisten die infiniten Zahlen, die einen unendlich großen Betrag haben, und die infinitesimalen Zahlen mit ihrem unendlich kleinen Betrag.
keine Erweiterung des reellen Zahlenkörpers. Wichtig ist, dass man mit den hyperreellen
Zahlen tatsächlich im Unendlichen rechnen kann. Dies leisten die infiniten Zahlen, die einen unendlich großen Betrag haben, und die infinitesimalen Zahlen mit ihrem unendlich kleinen Betrag.Du weißt, dass man die hyperreellen Zahlen mittels reeller Zahlenfolgen beschreibt. Und die Rechengesetze werden von
 nach
nach  übertragen, weil
die Rechenoperationen gliedweise mit den Folgengliedern jeweils gleicher Nummer durchgeführt werden. Nehmen wir einmal die drei Beispielzahlen
übertragen, weil
die Rechenoperationen gliedweise mit den Folgengliedern jeweils gleicher Nummer durchgeführt werden. Nehmen wir einmal die drei Beispielzahlen7 = (7 ; 7 ; 7 ; 7 ; 7 ; 7 ; ... ),
 = (1 ; 2 ; 3 ; 4 ; 5 ; 6 ; ... ) und
= (1 ; 2 ; 3 ; 4 ; 5 ; 6 ; ... ) und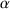 = (0,1 ; 0,01 ; 0,001 ; 0,0001 ; 0,00001 ; 0,000001 ; ... ) .
= (0,1 ; 0,01 ; 0,001 ; 0,0001 ; 0,00001 ; 0,000001 ; ... ) .Wo würdest Du diese Zahlen auf der Zahlengeraden suchen?
F: Nun ja, bei 7 ist es klar. Weil es sich um eine konstante Folge handelt, ist dies die reelle Zahl Sieben.
 ist größer als jede reelle Zahl, denn
bei jedem Vergleich mit irgendeiner reellen Zahl besitzt sie unendlich viele Folgenglieder, die größer sind, aber nur endlich viele, die kleiner sind.
ist größer als jede reelle Zahl, denn
bei jedem Vergleich mit irgendeiner reellen Zahl besitzt sie unendlich viele Folgenglieder, die größer sind, aber nur endlich viele, die kleiner sind.
 ist also eine infinite Zahl.
Und
ist also eine infinite Zahl.
Und 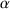 ist eine infinitesimale Zahl, denn hier liefert ein Vergleich
mit einer reellen Zahl, dass unendlich viele Folgenglieder von alpha kleiner ...
ist eine infinitesimale Zahl, denn hier liefert ein Vergleich
mit einer reellen Zahl, dass unendlich viele Folgenglieder von alpha kleiner ...A: ... Auch beim Vergleich mit –8?
F: Ich war ungenau. Um festzustellen, von welchem Typ eine hyperreelle Zahl ist, muss man ihren Betrag betrachten.
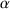 ist also deswegen
infinitesimal, weil bei jedem Vergleich mit einer reellen Zahl die Beträge unendlich vieler Folgenglieder von
ist also deswegen
infinitesimal, weil bei jedem Vergleich mit einer reellen Zahl die Beträge unendlich vieler Folgenglieder von 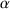 kleiner sind, aber höchstens endlich
viele betragsmäßig größer. Diese Begründung trifft auch beim Vergleich zum Beispiel mit -0,00024 zu.
kleiner sind, aber höchstens endlich
viele betragsmäßig größer. Diese Begründung trifft auch beim Vergleich zum Beispiel mit -0,00024 zu.A: Nun addiere jeweils zwei von ihnen und gib die Summenfolgen an.
F: Das ist einfach. Die Addition
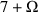 ergibt die
Zahlenfolge (8 ; 9 ; 10 ; 11 ; 12 ; 13 ; ... ) , bei
ergibt die
Zahlenfolge (8 ; 9 ; 10 ; 11 ; 12 ; 13 ; ... ) , bei 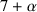 erhält man (7,1 ; 7,01 ; 7,001 ; 7,0001 ; 7,00001 ; 7,000001 ; ... ) ,
und
erhält man (7,1 ; 7,01 ; 7,001 ; 7,0001 ; 7,00001 ; 7,000001 ; ... ) ,
und 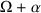 führt auf (1,1 ; 2,01 ; 3,001 ; 4,0001 ; 5,00001 ; 6,000001 ; ... ) .
führt auf (1,1 ; 2,01 ; 3,001 ; 4,0001 ; 5,00001 ; 6,000001 ; ... ) .A: Kannst Du auch von diesen Summenzahlen sagen, wo sie auf der Zahlengeraden zu finden sind?
F:
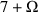 ist infinit, und
ist infinit, und 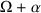 ist es ebenfalls. Bei
ist es ebenfalls. Bei 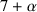 kann ich zumindest sagen, dass diese Summe nicht infinit ist. Sie ist aber auch nicht infinitesimal.
Und reell kann sie ebenfalls nicht sein, denn die sie beschreibende Folge ist nicht konstant.
kann ich zumindest sagen, dass diese Summe nicht infinit ist. Sie ist aber auch nicht infinitesimal.
Und reell kann sie ebenfalls nicht sein, denn die sie beschreibende Folge ist nicht konstant.A: Das hast Du richtig erkannt. Betrachten wir
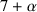 etwas genauer. Zahlen dieses Typs nennt man finit, also das Gegenteil von infinit.
Diese Zahl unterscheidet sich aber von der Zahl 7 nur infinitesimal. Deswegen sagt man auch,
etwas genauer. Zahlen dieses Typs nennt man finit, also das Gegenteil von infinit.
Diese Zahl unterscheidet sich aber von der Zahl 7 nur infinitesimal. Deswegen sagt man auch, 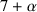 ist infinitesimal benachbart zur 7.
ist infinitesimal benachbart zur 7. F: Wenn ich zwei reelle Zahlen vergleiche, kann ich immer sagen, ob sie gleich sind oder welche von beiden die größere ist. Bei den drei Zahlen 7,
 und
und 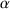 fällt der Vergleich auch nicht schwer, weil jede einem anderen Zahltyp angehört.
Wie kann ich denn bei zwei infiniten oder zwei infinitesimalen Zahlen entscheiden, welche die größere ist oder ob sie gleich sind?
fällt der Vergleich auch nicht schwer, weil jede einem anderen Zahltyp angehört.
Wie kann ich denn bei zwei infiniten oder zwei infinitesimalen Zahlen entscheiden, welche die größere ist oder ob sie gleich sind?A: Dazu braucht man jeweils Folgen, die die zu vergleichenden Zahlen beschreiben. Ordne doch bitte die folgenden vier Zahlen
 ,
, 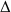 ,
, 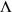 und
und  (Gamma, Delta, Lambda und Omega) der Größe nach, beginnend mit der kleinsten Zahl:
(Gamma, Delta, Lambda und Omega) der Größe nach, beginnend mit der kleinsten Zahl: = (10,0 ; 10,5 ; 11,0 ; 11,5 ; 12,0 ; 12,5 ; ... ) ,
= (10,0 ; 10,5 ; 11,0 ; 11,5 ; 12,0 ; 12,5 ; ... ) ,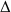 = (0,5 ; 1,0 ; 1,5 ; 2,0 ; 2,5 ; 3,0 ; ... ) ,
= (0,5 ; 1,0 ; 1,5 ; 2,0 ; 2,5 ; 3,0 ; ... ) ,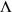 = (1 ; 3 ; 5 ; 7 ; 9 ; 11 ; ... ) .
= (1 ; 3 ; 5 ; 7 ; 9 ; 11 ; ... ) . = (1 ; 2 ; 3 ; 4 ; 5 ; 6 ; ... ) ,
= (1 ; 2 ; 3 ; 4 ; 5 ; 6 ; ... ) ,F: Einen Moment bitte, ich muss überlegen..... Hier ist die Lösung:
Es ist
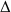 <
<  <
<  <
< 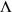 .
. A: Dein Ergebnis ist richtig, aber Du solltest es auch begründen. Erläutere bitte, wie Du es herausgefunden hast.
F: Ich muss eine Gesetzmäßigkeit herausfinden, wie die Folgen vermutlich weitergehen, welche Folgenglieder also die nächsten sind, denn die hier aufgeführten Folgenglieder täuschen.
A: Das stimmt. Normalerweise gibt man für Folgen auch diese Gesetzmäßigkeit an und erfasst damit sämtliche Folgenglieder auf einmal, nicht nur die ersten. Darauf will ich aber an dieser Stelle nicht weiter eingehen. Nun, wie hast Du die richtige Anordnung der vier infiniten Zahlen herausgefunden?
F: Nun ja,
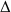 ist die kleinste Zahl, denn zum einen sind die Folgenglieder im Vergleich bei jeder Nummer am kleinsten,
und außerdem wachsen diese Folgenglieder offensichtlich in 0,5er-Schritten an. Letzteres gilt auch für
ist die kleinste Zahl, denn zum einen sind die Folgenglieder im Vergleich bei jeder Nummer am kleinsten,
und außerdem wachsen diese Folgenglieder offensichtlich in 0,5er-Schritten an. Letzteres gilt auch für  .
Zwar sind alle aufgeführten Folgenglieder mit gleicher Nummer jeweils die größten, weil aber jedes Folgenglied immer nur um 0,5 größer ist als sein Vorgänger, „überholen” die Folgenglieder von
.
Zwar sind alle aufgeführten Folgenglieder mit gleicher Nummer jeweils die größten, weil aber jedes Folgenglied immer nur um 0,5 größer ist als sein Vorgänger, „überholen” die Folgenglieder von
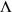 und
und  die Folgenglieder von
die Folgenglieder von
 . Also sind nur endlich viele Folgenglieder von
. Also sind nur endlich viele Folgenglieder von  größer,
aber unendlich viele Folgenglieder kleiner. Demzufolge ist
größer,
aber unendlich viele Folgenglieder kleiner. Demzufolge ist  <
< 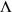 und
und  <
<  .
. Mit derselben Überlegung ist schließlich
 <
< 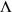 .
. A: Völlig richtig. Dann kannst Du sicherlich auch die folgenden vier Infinitesimalzahlen richtig anordnen.
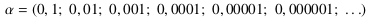 ,
,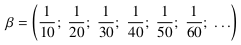 ,
,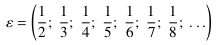 ,
,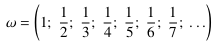 .
.F: Nun ja, mit ähnlichen Überlegungen erhalte ich ....
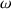 >
>  >
> 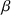 >
> 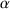
A: Das stimmt auch.
Solche Untersuchungen sind aber für die Analysis nicht wichtig. Im Grunde genügt es zu wissen, ob ein hyperreeller Term finit, infinit oder infinitesimal ist. Denn weil wir Analysis der reellen Funktionen betreiben, wird am Ende immer der reelle Teil des Terms gebildet.
Diese grundsätzlichen Überlegungen werden wir im zweiten Teil des Tutorials über das Rechnen in
 besprechen.
besprechen.





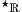 – Teil 1
– Teil 1