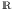FAQ - Frequently Asked Questions
Die Zahlengerade
- Was hat die Zahlengerade mit Zahlen zu tun?
- Zahlen sind Gebilde der Arithmetik, also der Rechenkunst, während Geraden Gebilde der Geometrie sind. Sie sind also verschiedene Dinge und haben zunächst nichts miteinander zu tun. Man kann aber die Größe von Zahlen und ihre Anordnung mit Hilfe von Geraden sehr gut veranschaulichen, indem man auf einem gezeichneten Geradenstück (mindestens) zwei Markierungen anbringt und sie mit den Zahlen kennzeichnet, für die die Markierungen stehen. Häufig sind dies die Zahlen Null und Eins dabei. Damit ist auch ein Maßstab festgelegt. Da man immer nur ein Geradenstück zeichnen kann, wird das Ende des Stücks, in dessen Richtung die Zahlen größer werden, mit einer Pfeilspitze versehen. Siehe auch das Tutorial über --> Zahlen und Lücken.
- Wie „dicht” ist die Zahlengerade mit Zahlen belegt?
- Das kommt darauf an, welche Zahlenmenge dargestellt wird. Bei den Mengen der natürlichen Zahlen
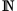 und der ganzen Zahlen
und der ganzen Zahlen 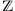 sind die Zahlen in gleichen Abständen wie auf einer Perlenschnur angeordnet. In den LÜcken zwischen ihnen liegen keine Zahlen. Dabei ist für
sind die Zahlen in gleichen Abständen wie auf einer Perlenschnur angeordnet. In den LÜcken zwischen ihnen liegen keine Zahlen. Dabei ist für 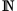 nicht einmal eine Gerade erforderlich, stattdessen spricht hier vom Zahlenstrahl.
nicht einmal eine Gerade erforderlich, stattdessen spricht hier vom Zahlenstrahl.
Bei den Mengen der rationalen Zahlen 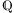 , der reellen Zahlen
, der reellen Zahlen  und der hyperreellen Zahlen
und der hyperreellen Zahlen 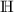 (bzw.
(bzw.  ) sind auch die Lücken zwischen den ganzen Zahlen dicht mit Zahlen belegt. Unter „dicht” muss man sich vorstellen, dass zwischen zwei vorgegebenen Zahlen der jeweiligen Menge immer beliebig viele weitere Zahlen dieser Menge liegen. Dass die Menge
) sind auch die Lücken zwischen den ganzen Zahlen dicht mit Zahlen belegt. Unter „dicht” muss man sich vorstellen, dass zwischen zwei vorgegebenen Zahlen der jeweiligen Menge immer beliebig viele weitere Zahlen dieser Menge liegen. Dass die Menge  mehr Zahlen enthält als
mehr Zahlen enthält als 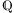 , liegt an den unterschiedlichen Verfahren, mit denen die Zahlen dieser Mengen gefunden werden (bis auf Division durch null uneingeschränkte Ausführung der Grundrechenarten bei
, liegt an den unterschiedlichen Verfahren, mit denen die Zahlen dieser Mengen gefunden werden (bis auf Division durch null uneingeschränkte Ausführung der Grundrechenarten bei 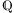 bzw. Grenzwerte konvergenter (Cauchy-)Folgen bei
bzw. Grenzwerte konvergenter (Cauchy-)Folgen bei  ). Die Menge
). Die Menge 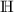 (bzw.
(bzw.  ) enthält schon allein deshalb mehr Zahlen als
) enthält schon allein deshalb mehr Zahlen als  , weil zu ihrer Konstruktion alle Folgen herangezogen werden, nicht nur die konvergenten.
, weil zu ihrer Konstruktion alle Folgen herangezogen werden, nicht nur die konvergenten.
Siehe auch das Tutorial über --> Zahlen und Lücken.
- Wo zeichnet man infinite und infinitesimale Zahlen auf der Zahlengeraden ein?
- Infinite Zahlen liegen von der Null unendlich weit weg. Will man zum Beispiel die infinite Zahl Γ gemeinsam mit der Null auf einem Blatt Papier darstellen, muss die Zahlengerade „schrumpfen”. Soll zum Beispiel Γ dort erscheinen, wo man sonst die Eins zeichnen würde, dann wendet man auf die Zahlengerade den Streckfaktor
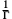 an. Dies hat zur Folge, dass alle finiten Zahlen nur infinitesimal von der Null entfernt zu denken sind, also in der Zeichnung mit der Null zusammenfallen. Es ist durchaus gerechtfertigt, statt „0” an dieser Stelle „
an. Dies hat zur Folge, dass alle finiten Zahlen nur infinitesimal von der Null entfernt zu denken sind, also in der Zeichnung mit der Null zusammenfallen. Es ist durchaus gerechtfertigt, statt „0” an dieser Stelle „ ” zu schreiben.
” zu schreiben.
Ganz entsprechend muss man die Zahlengerade mit dem infiniten Faktor 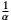 „strecken”, damit die infinitesimale Zahl
„strecken”, damit die infinitesimale Zahl 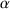 dort erscheint, wo man sonst die Eins zeichnen würde. Die Null ist dann die einzige reelle Zahl, die in diesem Maßstab gezeichnet werden kann; alle anderen finiten Zahlen, also auch die reellen, sind unendlich weit weggerückt. Siehe auch das Tutorial über die --> Zahlengerade in
dort erscheint, wo man sonst die Eins zeichnen würde. Die Null ist dann die einzige reelle Zahl, die in diesem Maßstab gezeichnet werden kann; alle anderen finiten Zahlen, also auch die reellen, sind unendlich weit weggerückt. Siehe auch das Tutorial über die --> Zahlengerade in ![ℝ]() .
.
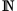 und der ganzen Zahlen
und der ganzen Zahlen 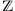 sind die Zahlen in gleichen Abständen wie auf einer Perlenschnur angeordnet. In den LÜcken zwischen ihnen liegen keine Zahlen. Dabei ist für
sind die Zahlen in gleichen Abständen wie auf einer Perlenschnur angeordnet. In den LÜcken zwischen ihnen liegen keine Zahlen. Dabei ist für 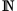 nicht einmal eine Gerade erforderlich, stattdessen spricht hier vom Zahlenstrahl.
nicht einmal eine Gerade erforderlich, stattdessen spricht hier vom Zahlenstrahl.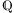 , der reellen Zahlen
, der reellen Zahlen  und der hyperreellen Zahlen
und der hyperreellen Zahlen 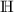 (bzw.
(bzw.  ) sind auch die Lücken zwischen den ganzen Zahlen dicht mit Zahlen belegt. Unter „dicht” muss man sich vorstellen, dass zwischen zwei vorgegebenen Zahlen der jeweiligen Menge immer beliebig viele weitere Zahlen dieser Menge liegen. Dass die Menge
) sind auch die Lücken zwischen den ganzen Zahlen dicht mit Zahlen belegt. Unter „dicht” muss man sich vorstellen, dass zwischen zwei vorgegebenen Zahlen der jeweiligen Menge immer beliebig viele weitere Zahlen dieser Menge liegen. Dass die Menge  mehr Zahlen enthält als
mehr Zahlen enthält als 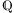 , liegt an den unterschiedlichen Verfahren, mit denen die Zahlen dieser Mengen gefunden werden (bis auf Division durch null uneingeschränkte Ausführung der Grundrechenarten bei
, liegt an den unterschiedlichen Verfahren, mit denen die Zahlen dieser Mengen gefunden werden (bis auf Division durch null uneingeschränkte Ausführung der Grundrechenarten bei 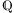 bzw. Grenzwerte konvergenter (Cauchy-)Folgen bei
bzw. Grenzwerte konvergenter (Cauchy-)Folgen bei  ). Die Menge
). Die Menge 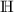 (bzw.
(bzw.  ) enthält schon allein deshalb mehr Zahlen als
) enthält schon allein deshalb mehr Zahlen als  , weil zu ihrer Konstruktion alle Folgen herangezogen werden, nicht nur die konvergenten.
, weil zu ihrer Konstruktion alle Folgen herangezogen werden, nicht nur die konvergenten.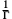 an. Dies hat zur Folge, dass alle finiten Zahlen nur infinitesimal von der Null entfernt zu denken sind, also in der Zeichnung mit der Null zusammenfallen. Es ist durchaus gerechtfertigt, statt „0” an dieser Stelle „
an. Dies hat zur Folge, dass alle finiten Zahlen nur infinitesimal von der Null entfernt zu denken sind, also in der Zeichnung mit der Null zusammenfallen. Es ist durchaus gerechtfertigt, statt „0” an dieser Stelle „ ” zu schreiben.
” zu schreiben.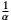 „strecken”, damit die infinitesimale Zahl
„strecken”, damit die infinitesimale Zahl 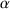 dort erscheint, wo man sonst die Eins zeichnen würde. Die Null ist dann die einzige reelle Zahl, die in diesem Maßstab gezeichnet werden kann; alle anderen finiten Zahlen, also auch die reellen, sind unendlich weit weggerückt. Siehe auch das Tutorial über die --> Zahlengerade in
dort erscheint, wo man sonst die Eins zeichnen würde. Die Null ist dann die einzige reelle Zahl, die in diesem Maßstab gezeichnet werden kann; alle anderen finiten Zahlen, also auch die reellen, sind unendlich weit weggerückt. Siehe auch das Tutorial über die --> Zahlengerade in .