FAQ - Frequently Asked Questions
Hyperreelle Zahlen
- Was ist der Unterschied zwischen „infinitesimal” und „infinit”?
- Infinite Zahlen besitzen einen unendlich großen Betrag. Weil in der Menge der hyperreellen Zahlen die Rechengesetze gelten, besitzt jede Zahl (außer Null natürlich) ihre Kehrzahl bezüglich der Multiplikation. Die Kehrzahl einer infiniten Zahl muss dann einen unendlich kleinen Betrag besitzen. Diese Kehrzahl liegt dann näher an der Null als jede reelle Zahl.
- Wie hängen infinite Zahlen mit infinitesimalen zusammen?
- Jede infinite Zahl besitzt ihre Kehrzahl. Das Produkt aus einer Zahl und ihrer Kehrzahl ist immer gleich eins. Also ist die Kehrzahl infinitesimal.
Ganz entsprechend ist die Kehrzahl einer infinitesimalen Zahl infinit.
- Gibt es infinitesimale reelle Zahlen?
- Ja, die Null besitzt diese Eigenschaft. Sie ist die einzige reelle Zahl, die gleichzeitig infinitesimal ist. Allerdings kann durch null nicht dividiert werden. Das Dividieren durch alle anderen infinitesimalen Zahlen ist dagegen möglich.
- Gibt es infinite reelle Zahlen?
- Nein, die gibt es nicht. Jede reelle Zahl, sei ihr Betrag auch noch so groß, ist endlich, also finit.
- Welche Arten hyperreeller Zahlen gibt es?
- Die Menge der hyperreellen Zahlen
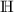 (oder
(oder  ) kann man leicht in verschiedene Zahltypen einteilen.
) kann man leicht in verschiedene Zahltypen einteilen.
- Was die Menge
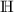 (bzw.
(bzw.  ) von der ursprünglichen Menge
) von der ursprünglichen Menge  unterscheidet, sind insbesondere die aktual unendlich großen infiniten Zahlen.
unterscheidet, sind insbesondere die aktual unendlich großen infiniten Zahlen.
- Ist eine Zahl nicht infinit, dann ist sie eine finite Zahl. Alle finiten Zahlen sind die Summe aus einem reellen Teil und einem infinitesimalen Teil. Bei ihnen kann man mehrere Untertypen unterscheiden.
- Ist der infinitesimale Teil gleich null, dann liegt eine reelle Zahl vor.
- Ist der reelle Teil gleich null, dann handelt es sich um eine infinitesimale Zahl. Ihr Betrag ist kleiner als der jeder reellen Zahl. Infinitesimale Zahlen sind die Kehrzahlen infiniter Zahlen.
- Die Zahl Null ist die einzige reelle Zahl, die auch infinitesimal ist.
- Warum schreibt man nichtreelle hyperreelle Zahlen mit Buchstaben, die wie Variable aussehen und nicht spezielle Symbole wie
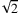 bei den irrationalen Zahlen?
bei den irrationalen Zahlen?
- Die irrationale Zahl
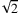 besitzt eine Schreibweise, der man sofort entnehmen kann, wie sie mit einer anderen Zahl, nämlich der natürlichen Zahl 2, zusammenhängt. Ihr Quadrat soll gleich 2 sein. Es handelt sich also um eine Termschreibweise, wobei das Wurzelzeichen
besitzt eine Schreibweise, der man sofort entnehmen kann, wie sie mit einer anderen Zahl, nämlich der natürlichen Zahl 2, zusammenhängt. Ihr Quadrat soll gleich 2 sein. Es handelt sich also um eine Termschreibweise, wobei das Wurzelzeichen 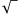 als stilisierter lateinischer Kleinbuchstabe „r” zu denken ist, was vom lateinischen Wort radix – Wurzel herkommt.
als stilisierter lateinischer Kleinbuchstabe „r” zu denken ist, was vom lateinischen Wort radix – Wurzel herkommt.
Andere irrationale Zahlen, für die solche einfachen algebraischen Zusammenhänge nicht gelten, bezeichnet man dagegen mit (möglichst einprägsamen) Buchstaben. Das bekannteste Beispiel ist die Kreiszahl 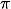 . Dieser griechische Kleinbuchstabe ist ausschließlich dieser Zahl vorbehalten. Ähnlich verhält es sich mit der von Euler beschriebenen Exponentialbasis e, was aber im Grunde eine Termschreibweise abkürzt (siehe weiter unten).
. Dieser griechische Kleinbuchstabe ist ausschließlich dieser Zahl vorbehalten. Ähnlich verhält es sich mit der von Euler beschriebenen Exponentialbasis e, was aber im Grunde eine Termschreibweise abkürzt (siehe weiter unten).
Es geht also darum, dass ein Leser an der Schreibweise einer Zahl sofort ihre Bedeutung erkennen kann. Deshalb verwendet man für infinitesimale Zahlen griechische Kleinbuchstaben (natürlich nie ein 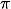 ) und für infinite Zahlen griechische Großbuchstaben. Leider entstehen dabei manchmal Verwechslungsmöglichkeiten, zum Beispiel wenn man die reelle Zählvariable N (lateinischer Buchstabe) ins infinite Hyperreelle fortsetzt, dort mit dem griechischen Großbuchstaben Ν (gesprochen „Nü”) geschrieben. Das Verständnis des Zusammenhangs ist also sehr wichtig. Die Exponentialbasis e in Termschreibweise ist dafür ein Beispiel:
) und für infinite Zahlen griechische Großbuchstaben. Leider entstehen dabei manchmal Verwechslungsmöglichkeiten, zum Beispiel wenn man die reelle Zählvariable N (lateinischer Buchstabe) ins infinite Hyperreelle fortsetzt, dort mit dem griechischen Großbuchstaben Ν (gesprochen „Nü”) geschrieben. Das Verständnis des Zusammenhangs ist also sehr wichtig. Die Exponentialbasis e in Termschreibweise ist dafür ein Beispiel:
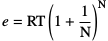
für infinites Ν.
- Was sind hypernatürliche Zahlen?
- Der Körper der hyperreellen Zahlen
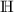 (oder
(oder  ) enthält infinite Zahlen. Mit ihnen wird der Körper
) enthält infinite Zahlen. Mit ihnen wird der Körper  mit all seinen Eigenschaften ins aktual Unendliche fortgesetzt. Damit muss es auch Zahlen geben, mit denen das Zählen ins Unendliche fortgesetzt werden kann. Man nennt sie hypernatürliche Zahlen. So wie der Körper
mit all seinen Eigenschaften ins aktual Unendliche fortgesetzt. Damit muss es auch Zahlen geben, mit denen das Zählen ins Unendliche fortgesetzt werden kann. Man nennt sie hypernatürliche Zahlen. So wie der Körper  die Menge
die Menge 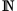 zum Zählen enthält, enthält der Körper
zum Zählen enthält, enthält der Körper 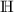 (bzw.
(bzw.  ) ganz entsprechend die Menge
) ganz entsprechend die Menge 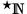 zum Zählen. Eine reelle Zahlenfolge, die eine hypernatürliche Zahl beschreibt, enthält bei genügend vielen Indizes natürliche Zahlen. Dafür ist
zum Zählen. Eine reelle Zahlenfolge, die eine hypernatürliche Zahl beschreibt, enthält bei genügend vielen Indizes natürliche Zahlen. Dafür ist
 = (1; 2; 3; 4; 5; 6; ...)
= (1; 2; 3; 4; 5; 6; ...)
ein Beispiel.
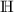 (oder
(oder  ) kann man leicht in verschiedene Zahltypen einteilen.
) kann man leicht in verschiedene Zahltypen einteilen.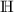 (bzw.
(bzw.  ) von der ursprünglichen Menge
) von der ursprünglichen Menge  unterscheidet, sind insbesondere die aktual unendlich großen infiniten Zahlen.
unterscheidet, sind insbesondere die aktual unendlich großen infiniten Zahlen.
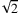 bei den irrationalen Zahlen?
bei den irrationalen Zahlen?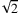 besitzt eine Schreibweise, der man sofort entnehmen kann, wie sie mit einer anderen Zahl, nämlich der natürlichen Zahl 2, zusammenhängt. Ihr Quadrat soll gleich 2 sein. Es handelt sich also um eine Termschreibweise, wobei das Wurzelzeichen
besitzt eine Schreibweise, der man sofort entnehmen kann, wie sie mit einer anderen Zahl, nämlich der natürlichen Zahl 2, zusammenhängt. Ihr Quadrat soll gleich 2 sein. Es handelt sich also um eine Termschreibweise, wobei das Wurzelzeichen 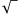 als stilisierter lateinischer Kleinbuchstabe „r” zu denken ist, was vom lateinischen Wort radix – Wurzel herkommt.
als stilisierter lateinischer Kleinbuchstabe „r” zu denken ist, was vom lateinischen Wort radix – Wurzel herkommt.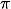 . Dieser griechische Kleinbuchstabe ist ausschließlich dieser Zahl vorbehalten. Ähnlich verhält es sich mit der von Euler beschriebenen Exponentialbasis e, was aber im Grunde eine Termschreibweise abkürzt (siehe weiter unten).
. Dieser griechische Kleinbuchstabe ist ausschließlich dieser Zahl vorbehalten. Ähnlich verhält es sich mit der von Euler beschriebenen Exponentialbasis e, was aber im Grunde eine Termschreibweise abkürzt (siehe weiter unten).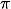 ) und für infinite Zahlen griechische Großbuchstaben. Leider entstehen dabei manchmal Verwechslungsmöglichkeiten, zum Beispiel wenn man die reelle Zählvariable N (lateinischer Buchstabe) ins infinite Hyperreelle fortsetzt, dort mit dem griechischen Großbuchstaben Ν (gesprochen „Nü”) geschrieben. Das Verständnis des Zusammenhangs ist also sehr wichtig. Die Exponentialbasis e in Termschreibweise ist dafür ein Beispiel:
) und für infinite Zahlen griechische Großbuchstaben. Leider entstehen dabei manchmal Verwechslungsmöglichkeiten, zum Beispiel wenn man die reelle Zählvariable N (lateinischer Buchstabe) ins infinite Hyperreelle fortsetzt, dort mit dem griechischen Großbuchstaben Ν (gesprochen „Nü”) geschrieben. Das Verständnis des Zusammenhangs ist also sehr wichtig. Die Exponentialbasis e in Termschreibweise ist dafür ein Beispiel: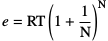
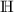 (oder
(oder  ) enthält infinite Zahlen. Mit ihnen wird der Körper
) enthält infinite Zahlen. Mit ihnen wird der Körper  mit all seinen Eigenschaften ins aktual Unendliche fortgesetzt. Damit muss es auch Zahlen geben, mit denen das Zählen ins Unendliche fortgesetzt werden kann. Man nennt sie hypernatürliche Zahlen. So wie der Körper
mit all seinen Eigenschaften ins aktual Unendliche fortgesetzt. Damit muss es auch Zahlen geben, mit denen das Zählen ins Unendliche fortgesetzt werden kann. Man nennt sie hypernatürliche Zahlen. So wie der Körper  die Menge
die Menge 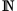 zum Zählen enthält, enthält der Körper
zum Zählen enthält, enthält der Körper 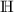 (bzw.
(bzw.  ) ganz entsprechend die Menge
) ganz entsprechend die Menge 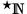 zum Zählen. Eine reelle Zahlenfolge, die eine hypernatürliche Zahl beschreibt, enthält bei genügend vielen Indizes natürliche Zahlen. Dafür ist
zum Zählen. Eine reelle Zahlenfolge, die eine hypernatürliche Zahl beschreibt, enthält bei genügend vielen Indizes natürliche Zahlen. Dafür ist = (1; 2; 3; 4; 5; 6; ...)
= (1; 2; 3; 4; 5; 6; ...)