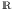FAQ - Frequently Asked Questions
Erweiterung des Zahlenkörpers ℝ
- Wie kann man überhaupt dem Körper der reellen Zahlen, der doch vollständig ist, noch weitere, z.B.
infinitesimale und infinite Zahlen hinzufügen?
- Für die Differentialrechnung benötigt man nur die infinitesimalen Zahlen; diese kann man schnell axiomatisch
einführen, indem man fordert, dass es mindestens eine infinitesimale Zahl gibt. Es lässt sich leicht zeigen,
dass es dann unendliche viele infinitesimale Zahlen geben muss.
(Vgl. unseren
--> MNU-Artikel zur Differenzialrechnung).
Für die Integralrechnung reicht das nicht aus: Infinite Zahlen lassen sich zwar als Kehrwerte von infinitesimalen
Zahlen erhalten, man braucht aber spezielle, sogenannte hypernatürliche Zahlen, da man beim Integrieren bis zu einer
höchsten infiniten Grenze zählen können muss. Spätestens hier müssen die hyperreellen Zahlen konstruiert werden.
Dies kann durch eine Konstruktion analog zu der der reellen Zahlen geschehen: Diese werden üblicherweise als
Äquivalenzklassen von rationalen Cauchy-Folgen (z.B. Intervallschachtelungen) definiert. Auch wenn man dabei reelle Zahlen
verwenden würde, bekäme man doch nur wieder die reellen Zahlen. In diesem Sinne sind diese abgeschlossen.
Wenn man aber die Beschränkung auf konvergente Folgen fallen lässt, erhält man mehr. Dazu muss zusätzlich die
Äquivalenzrelation für Folgen erweitert werden, so dass auch unendlich viele Ausnahmen für die Äquivalenz
irrelevant sein können. (Genaueres dazu finden Sie u.a. in unserem
--> MNU-Artikel zur Integralrechnung und unserem
--> Buch zur Nichtstandard-Analysis.)
- Worauf ist bei einer Zahlbereichserweiterung zu achten?
- Jede Zahlbereichserweiterung besteht aus vier Teilen.
- Zunächst muss als Grundlage ein Zahlbereich vorhanden sein.
- Aus den vorhandenen Zahlen werden neue Objekte nach einem definierten Verfahren konstruiert.
- Nach dem Permanenzprinzip müssen die neuen Objekte so konstruiert werden, dass mit ihnen nach den bisher gültigen Gesetzen gerechnet werden kann.
Im allgemeinen erweisen sich verschiedene neue Objekte als zum Rechnen gleichwertig. Es werden daher Äquivalenzklassen gebildet. Es muss dann nachgewiesen werden, dass Objekte, die als äquivalent definiert wurden, trotz ihrer Verschiedenheit zum selben Rechenergebnis führen.
- Die ursprüngliche Zahlenmenge muss mit einer Teilmenge des neuen Bereichs identifiziert werden, damit von einer Zahlbereichserweiterung gesprochen werden kann.
- Was ist gemeint, wenn man eine Menge als „abgeschlossen”, „vollständig” oder dergleichen bezeichnet?
- Jede Erweiterung eines vorhandenen Zahlbereichs beruht auf einem für diesen Zweck festgelegten Verfahren. So erweitert man die Menge natürlichen Zahlen
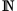 zur Menge der rationalen Zahlen
zur Menge der rationalen Zahlen 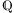 , indem man fordert, alle Grundrechenarten sollen uneingeschränkt ausführbar sein (mit Ausnahme der Division durch null). Wendet man die Grundrechenarten auch auf rationale Zahlen an, erhält man wieder nur rationale Zahlen. Bezüglich dieses Verfahrens bezeichnet man die Menge
, indem man fordert, alle Grundrechenarten sollen uneingeschränkt ausführbar sein (mit Ausnahme der Division durch null). Wendet man die Grundrechenarten auch auf rationale Zahlen an, erhält man wieder nur rationale Zahlen. Bezüglich dieses Verfahrens bezeichnet man die Menge 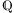 deshalb als abgeschlossen.
deshalb als abgeschlossen.
Mit Hilfe von Intervallschachtelungen (oder Grenzwerten konvergenter Folgen) rationaler Zahlen findet man irrationale Zahlen. Dieses Verfahren unterscheidet sich also von den Grundrechenarten und liefert diese zusätzlichen Zahlen. Auf diese Weise erweitert man die Menge 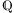 zur größeren Menge
zur größeren Menge  , denn auch mit Intervallschachtelungen aus irrationalen Zahlen findet man wieder nur irrationale Zahlen. Deshalb bezeichnet man die Menge
, denn auch mit Intervallschachtelungen aus irrationalen Zahlen findet man wieder nur irrationale Zahlen. Deshalb bezeichnet man die Menge  als vollständig.
als vollständig.
Mit einem anderen Verfahren kann man nun der Menge  zusätzliche Zahlen hinzufügen und sie zur Menge
zusätzliche Zahlen hinzufügen und sie zur Menge 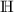 (oder
(oder  ) der hyperreellen Zahlen erweitern. Zu ihrer Konstruktion sind alle Folgen reeller Zahlen (nicht nur die konvergenten) zugelassen. Allein deshalb ist die Menge
) der hyperreellen Zahlen erweitern. Zu ihrer Konstruktion sind alle Folgen reeller Zahlen (nicht nur die konvergenten) zugelassen. Allein deshalb ist die Menge 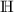 (bzw.
(bzw.  ) größer als
) größer als  . Mit diesem Verfahren findet man alle hyperreellen Zahlen, weswegen auch hier Begriffe wie abgeschlossen oder vollständig zutreffen.
. Mit diesem Verfahren findet man alle hyperreellen Zahlen, weswegen auch hier Begriffe wie abgeschlossen oder vollständig zutreffen.
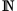 zur Menge der rationalen Zahlen
zur Menge der rationalen Zahlen 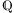 , indem man fordert, alle Grundrechenarten sollen uneingeschränkt ausführbar sein (mit Ausnahme der Division durch null). Wendet man die Grundrechenarten auch auf rationale Zahlen an, erhält man wieder nur rationale Zahlen. Bezüglich dieses Verfahrens bezeichnet man die Menge
, indem man fordert, alle Grundrechenarten sollen uneingeschränkt ausführbar sein (mit Ausnahme der Division durch null). Wendet man die Grundrechenarten auch auf rationale Zahlen an, erhält man wieder nur rationale Zahlen. Bezüglich dieses Verfahrens bezeichnet man die Menge 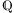 deshalb als abgeschlossen.
deshalb als abgeschlossen.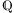 zur größeren Menge
zur größeren Menge  , denn auch mit Intervallschachtelungen aus irrationalen Zahlen findet man wieder nur irrationale Zahlen. Deshalb bezeichnet man die Menge
, denn auch mit Intervallschachtelungen aus irrationalen Zahlen findet man wieder nur irrationale Zahlen. Deshalb bezeichnet man die Menge  als vollständig.
als vollständig. zusätzliche Zahlen hinzufügen und sie zur Menge
zusätzliche Zahlen hinzufügen und sie zur Menge 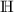 (oder
(oder  ) der hyperreellen Zahlen erweitern. Zu ihrer Konstruktion sind alle Folgen reeller Zahlen (nicht nur die konvergenten) zugelassen. Allein deshalb ist die Menge
) der hyperreellen Zahlen erweitern. Zu ihrer Konstruktion sind alle Folgen reeller Zahlen (nicht nur die konvergenten) zugelassen. Allein deshalb ist die Menge 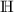 (bzw.
(bzw.  ) größer als
) größer als  . Mit diesem Verfahren findet man alle hyperreellen Zahlen, weswegen auch hier Begriffe wie abgeschlossen oder vollständig zutreffen.
. Mit diesem Verfahren findet man alle hyperreellen Zahlen, weswegen auch hier Begriffe wie abgeschlossen oder vollständig zutreffen.