Beispiele zur Analysis mit hyperreellen Zahlen
Hyperreelle Zahlen und das Rechnen mit ihnen
In der Zahlenmenge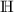 (bzw.
(bzw.  ) gelten dieselben Rechengesetze wie in
) gelten dieselben Rechengesetze wie in  . Umfassendere Informationen zum Rechnen in
. Umfassendere Informationen zum Rechnen in 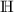 (bzw.
(bzw.  ) bieten die beiden Tutorials --> Rechnen in
) bieten die beiden Tutorials --> Rechnen in  – Teil 1 und --> Rechnen in
– Teil 1 und --> Rechnen in  – Teil 2. In letzterem findet man auch die Rechentabellen für hyperreelle Zahlen.
– Teil 2. In letzterem findet man auch die Rechentabellen für hyperreelle Zahlen.Sofern in den folgenden Beispielen Folgen benutzt werden, um hyperreelle Zahlen zu beschreiben, dann werden die Folgen sowohl als geschlossener Ausdruck, zum Beispiel (2n), als auch mittels Aufzählung der ersten Folgenglieder, zum Beispiel (2; 4; 6; 8; 10; 12; …), angegeben. Die Indexmenge ist immer
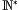 .
.
- Hyperreelle Zahlen als Folgen reeller Zahlen
- Hyperreelle Zahlen werden mittels Folgen reeller Zahlen beschrieben. Dafür sind sämtliche Folgen zugelassen.
- Konstante Folgen beschreiben hyperreelle Zahlen, die auch reell sind:
(−13; −13; −13; −13; −13; …) = (−13) = −13,
(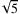 ;
;
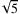 ;
;
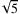 ;
;
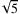 ;
;
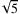 ; …) =
(
; …) =
(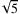 ) =
) =
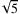 ,
,
(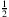 ;
;
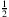 ;
;
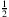 ;
;
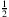 ;
;
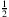 ; …) =
(
; …) =
(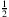 ) =
) =
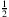 .
.
- Die Folge (0,4; 0,49; 0,499; 0,4999; 0,49999; 0,499999; …) = (0,5 − 10-n) ist nicht konstant, aber offenbar beschränkt, denn sie überschreitet nicht die Zahl
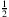 . Deswegen steht sie für eine Zahl, die finit, aber nicht reell ist. Sie ist aber infinitesimal benachbart zu
. Deswegen steht sie für eine Zahl, die finit, aber nicht reell ist. Sie ist aber infinitesimal benachbart zu 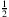 ,
,
- denn die Differenz beider Zahlen ergibt, wenn man Folgenglieder mit jeweils gleicher Nummer voneinander subtrahiert, (0,1; 0,01; 0,001; 0,0001; 0,00001; …) = (10-n) = α. Diese Folge steht für eine infinitesimale Zahl.
- Die Folge (1; 2,1; 3,2; 4,3; 5,4; 6,5; …) = (n + 0,1⋅(n − 1)) steht für eine infinite Zahl, denn sie ist nicht beschränkt.
- Die Folge (3; 4; 5; 6; 7; 8; …) = (n+2) steht ebenfalls für eine infinite Zahl. Sie besitzt nur natürliche Zahlen als Folgenglieder. Diese Eigenschaft besitzt sie auch im Infiniten, sie ist eine hypernatürliche Zahl.
- Konstante Folgen beschreiben hyperreelle Zahlen, die auch reell sind:
- Rechnen mit hyperreellen Zahlen als Rechnen mit ihren reellen Zahlenfolgen
- In diesem Beispiel wird mit den drei (hyperreellen) Zahlen gerechnet, das sind
die auch reelle Zahl 4 = (4) = (4; 4; 4; 4; 4; 4; ...),
die infinite Zahl Ω = (n) = (1; 2; 3; 4; 5; 6; ...),
die infinitesimale Zahl δ = (5⋅10-n) = (0,5; 0,05; 0,005; 0,0005; 0,00005; 0,000005; ...).
Dazu werden ihre beschreibenden reellen Zahlenfolgen gliedweise auf die entsprechende Weise verknüpft. Weitere Beispiele gibt es im Tutorial über das --> Rechnen in – Teil 1.
– Teil 1.
- 4 + Ω = (4) + (n) = (4+n) = (5; 6; 7; 8; 9; 10; ...) ist infinit.
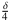 = (0,125; 0,0125; 0,00125; 0,000125; 0,0000125; 0,00000125; ...) ist infinitesimal.
= (0,125; 0,0125; 0,00125; 0,000125; 0,0000125; 0,00000125; ...) ist infinitesimal.
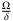 = (2; 40; 600; 8000; 100000; 1200000; ...) ist infinit.
= (2; 40; 600; 8000; 100000; 1200000; ...) ist infinit.
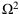 = (1; 4; 9; 16; 32; 64; ...) ist infinit.
= (1; 4; 9; 16; 32; 64; ...) ist infinit.
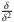 = (2; 20; 200; 2000; 20000; 200000; ...) ist infinit.
= (2; 20; 200; 2000; 20000; 200000; ...) ist infinit.
- 4 − Ω = (3; 2; 1; 0; −1; −2; ...) ist (negativ) infinit.
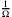 =
= 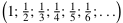 ist infinitesimal.
ist infinitesimal.
- Größenordnung des Ergebnisses
- Im Tutorial über das --> Rechnen in
 – Teil 2 stehen die Verknüpfungstabellen der verschiedenen hyperreellen Zahltypen. Dort werden auch diejenigen Fälle erläutert, in denen ohne genauere Kenntnis der beteiligten Zahlen die Größenordnung des Ergebisses nicht angegeben werden kann.
– Teil 2 stehen die Verknüpfungstabellen der verschiedenen hyperreellen Zahltypen. Dort werden auch diejenigen Fälle erläutert, in denen ohne genauere Kenntnis der beteiligten Zahlen die Größenordnung des Ergebisses nicht angegeben werden kann. - Bestandteile finiter hyperreeller Zahlen – Eindeutigkeit
- Jede finite hyperreelle Zahl setzt sich eindeutig aus einem reellen Teil und einem infinitesimalen Teil zusammen.
Denn nimmt man an, für eine Zahl a gäbe es zwei verschiedene Zerlegungen r + α und s + β (r und s reell, α und β infinitesimal), dann würde gelten
r + α = s + β,
was man umformen kann zu
r − s = β − α.
Auf der linken Seite steht eine reelle Zahl, auf der rechten Seite eine infinitesimale. Die Null ist die einzige Zahl, die sowohl reell als auch infinitesimal ist, also gilt
r = s und α = β. Die Zerlegung ist somit eindeutig. - Reeller Teil einer hyperreellen Zahl – Verträglichkeit mit den Grundrechenarten
- Es seien jeweils a = r + α und b = s + β zwei finite hyperreelle Zahlen mit den reellen Teilen r bzw. s und den infinitesimalen Teilen α bzw. β. Für die Grundrechenarten gilt dann jeweils das folgende.
- Addition: Der reelle Teil einer Summe ist gleich der Summe der reellen Teile seiner Summanden.
RT(a + b) = RT[(r + α) + (s + β)] = RT[(r + s) + (α + β)] = r + s = RT(a) + RT(b). - Subtraktion: Der reelle Teil einer Differenz ist gleich der Differenz der reellen Teile von Minuend und Subtrahend.
RT(a − b) = RT[(r + α) − (s + β)] = RT[(r − s) + (α − β)] = r − s = RT(a) − RT(b). - Multiplikation: Der reelle Teil eines Produkts ist gleich dem Produkt der reellen Teile seiner Faktoren.
RT(a ⋅ b) = RT[(r + α) ⋅ (s + β)] = RT[(r ⋅ s) + (r ⋅ β) + (α ⋅ s) + (α ⋅ β)]
= r ⋅ s = RT(a) ⋅ RT(b). - Division: Der reelle Teil eines Quotienten ist gleich dem Quotienten aus den reellen Teilen von Dividend und Divisor.
Bei der Division ist es einfacher, wenn man nachweist, dass die Differenz aus dem Quotienten zweier finiter Zahlen und dem Quotienten der jeweiligen reellen Teile infinitesimal ist. Zusätzlich ist hier s ≠ 0 zu fordern, dann gilt
![(a⁄b) − (r⁄s) = (r + α)⁄(s + β) − r⁄s = [(r + α)s − r(s + β)]⁄[(s + β)s] = [(rs) + (αs) − (rs) − (rβ)]⁄[s(s + β)] = [(αs) − (rβ)]⁄[s^2 + (sβ)]](Gleichungen/Beispiel-RT-Division-Gl1.png) .
.
Der Zähler im letzten Term ist infinitesimal, der Nenner ist es nicht, also ist der Bruch infinitesimal.
- Addition: Der reelle Teil einer Summe ist gleich der Summe der reellen Teile seiner Summanden.
- Hyperreelle Terme
- In den folgenden Beispielen haben die Buchstaben wie üblich die folgende Bedeutung:
-- Γ, Δ, Λ usw. (griechische Großbuchstaben) für infinite Zahlen,
-- α, β, γ usw. (griechische Kleinbuchstaben) für infinitesimale Zahlen.
Dabei sind entsprechende Groß- und Kleinbuchstaben jeweils Kehrwerte voneinander, zum Beispiel ω =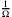 .
.
- 24 + 3α:
Die Summe ist (positiv) finit, infinitesimal benachbart zu 24. - 2413,8 − Γ:
Die Differenz ist (negativ) infinit. - α ⋅ Δ:
Über die Größenordnung des Produkts kann ohne genauere Informationen zu den beteiligten Faktoren nichts ausgesagt werden. - 0,004 − 27α:
Die Differenz ist (positiv) finit. - δ ⋅ Δ2:
Das Produkt ist gleich Δ, ist also infinit, je nach Vorzeichen positiv oder negativ. 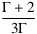
ist (positiv) finit, denn es kann umgeformt werden zu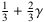
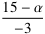
ist (negativ) finit, denn es kann umgeformt werden zu −5 +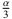
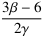
ist auf jeden Fall (negativ) infinit, unabhängig von der Größenordnung der infinitesimalen Zahlen.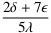
ist finit, infinit oder infinitesimal je nach Größenordnung der beteiligten infinitesimalen Zahlen.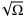
ist infinit, denn wäre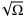 finit, könnte das Produkt
finit, könnte das Produkt 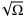 ⋅
⋅ 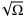 nicht infinit sein.
nicht infinit sein.
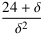
ist infinit, denn es kann umgeformt werden zu 24⋅Δ2 + Δ.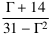
ist (negativ) infinitesimal, denn der Nenner ist gegenüber dem Zähler „doppelt” infinit.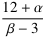
ist infinitesimal benachbart zu −4.
- 24 + 3α:





