Differentialrechnung
- Steigung des Graphen der Funktion f mit f(x)=x3 im Punkt P(2;8)
- Die reelle Funktion f werde zunächst ins Hyperreelle erweitert. Auf dem Graphen liegt zum Punkt P(2;8) der Punkt Q(2+α;(2+α)3) infinitesimal benachbart, denn α sei infinitesimal. Dann erhält man für die Steigung zwischen P und Q
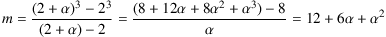 .
.
Der reelle Teil davon ist die gesuchte Steigung des Graphen bzw. die Ableitung der Funktion f an der Stelle x=2:
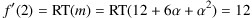 .
.
- Ableitung der Quadratfunktion
- Auf dem Graphen der (hyperreell erweiterten) Funktion f mit f(x)=x2 sei der Punkt P(x;x2) beliebig angenommen. Im infinitesimalen x-Abstand davon liege der Punkt Q(x+α;(x+α)2), denn α sei infinitesimal. Für die Steigung zwischen P und Q erhält man dann
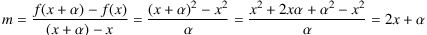 .
.
Der reelle Teil davon ist die gesuchte Ableitung f' der Funktion f:
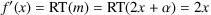 .
.
- Summenregel der Differentialrechnung
- Es seien f und g zwei differenzierbare Funktionen mit den Ableitungen f' bzw. g'. Dann erält man die Ableitung der Summenfunktion f+g mit (f+g)(x) = f(x) + g(x) folgendermaßen:
![(f+g)'(x) = RT{ [ (f+g)(x+α) - (f+g)(x) ] ⁄ [ (x+α)-x ] }](Gleichungen/Beispiel-Summenregel-Gl1.png)
![= RT{ [ f(x+α)+g(x+α) - ( f(x)+g(x) ) ] ⁄ α }](Gleichungen/Beispiel-Summenregel-Gl2.png)
![= RT{ [ f(x+α)-f(x) ]⁄α + [ g(x+α)-g(x) ]⁄α }](Gleichungen/Beispiel-Summenregel-Gl3.png)
![= RT{ [ f(x+α)-f(x) ]⁄α } + RT{ [ g(x+α)-g(x) ]⁄α }](Gleichungen/Beispiel-Summenregel-Gl4.png)
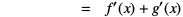 .
.
- Potenzregel der Differentialrechnung
- Die Potenzfunktion pn mit pn(x) = xn mit n > 1, n ∈
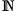 ist differenzierbar. Man erhält für die Steigung zwischen zwei infinitesimal benachbarten Punkten P(x ; xn) und Q(x+α ; (x+α)n)
ist differenzierbar. Man erhält für die Steigung zwischen zwei infinitesimal benachbarten Punkten P(x ; xn) und Q(x+α ; (x+α)n)
![m = [(x+α)^n - x^n]⁄[(x+α) - x]](Gleichungen/Beispiel-Potenzregel-Gl1.png)
![= [x^n + n⋅x^(n−1)⋅α + (Summanden mit mindestens α^2) − x^n]⁄[α]](Gleichungen/Beispiel-Potenzregel-Gl2.png)
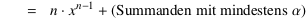 .
.
Der reelle Teil davon ist die Ableitung der Funktion:
![p_n'(x) = RT[n⋅x^(n-1) + (Summanden mit mindestens α)] = n⋅x^(n-1)](Gleichungen/Beispiel-Potenzregel-Gl4.png) .
.
- Produktregel der Differentialrechnung
- Sei die Funktion f das Produkt zweier differenzierbarer Funktionen u und v, also
f(x) = y = (u ⋅ v)(x) = u(x) ⋅ v(x).
Verändert man x um ein infinitesimales dx, dann ändern sich u um du und v um dv, wobei wegen der Differenzierbarkeit der beiden Faktorfunktionen du und dv jeweils infinitesimal sind. Für die Änderung dy des Produkts erhält man dann
dy = (u + du)⋅(v + dv) − u⋅v = u⋅v + u⋅dv + du⋅v + du⋅dv − u⋅v
und schließlich den Differentailquotienten
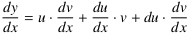 .
.
Der reelle Teil davon ist die Ableitung der Produktfunktion:
![(u⋅v)'(x) = RT[(dy)⁄(dx)] = (u)⋅RT[(dv)⁄(dx)] + RT[(du)⁄(dx)]⋅(v) + RT[(du)⋅(dv)⁄(dx)]](Gleichungen/Beispiel-Produktregel-Gl2.png)
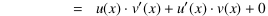 ,
,
denn der letzte Summand ist infinitesimal.
- Kettenregel der Differentialrechnung
- Gegeben sei die Verkettung f2 ○ f1 zweier differenzierbarer, also stetiger Funktionen f1 und f2 und es gelte (f2 ○ f1)(x) = f2(f1(x)) := f(x). Die Funktion f1 bildet also ein vorgegebenes x auf einen Zwischenwert z ab, der sofort von f2 zu y weiterverarbeitet wird.
Verändert man nun x um ein infinitesimales h, so ändert die stetige Funktion f1 das Bild z um ein ebenfalls infinitesimals k, wobei auch k = 0 auftreten kann. Dabei gilt 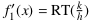 .
.
Die Funktion f2 verarbeitet den Zwischenwert z weiter zu y. Eine Veränderung von z um ein infinitesimales k bewirkt hier eine infinitesimale Veränderung von y um v. Es gilt entsprechend 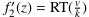 . Gesucht ist
. Gesucht ist 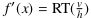 .
.
- Fall: k ≠ 0. In diesem Fall kann man den Bruch
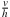 mit dem infinitesimalen k erweitern und erhält
mit dem infinitesimalen k erweitern und erhält
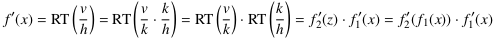 .
.
- Fall: k = 0. Hier ändert sich f1(x) bei infinitesimaler Änderung von x nicht, also bleibt auch f2(z) unverändert. Daher sind die beiden Quotienten
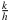 und
und 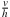 null, was sogar deren reelle Teile sind. Also gilt auch f1'(x) = 0 und f'(x) = 0 und die Ableitung der Verkettung ist in der Form 0 = f'(x) = f2'(f1(x)) ⋅ 0 dieselbe wie im 1. Fall.
null, was sogar deren reelle Teile sind. Also gilt auch f1'(x) = 0 und f'(x) = 0 und die Ableitung der Verkettung ist in der Form 0 = f'(x) = f2'(f1(x)) ⋅ 0 dieselbe wie im 1. Fall.
<nach oben>
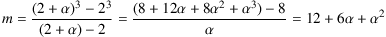 .
.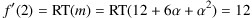 .
.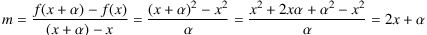 .
.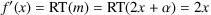 .
.
![(f+g)'(x) = RT{ [ (f+g)(x+α) - (f+g)(x) ] ⁄ [ (x+α)-x ] }](Gleichungen/Beispiel-Summenregel-Gl1.png)
![= RT{ [ f(x+α)+g(x+α) - ( f(x)+g(x) ) ] ⁄ α }](Gleichungen/Beispiel-Summenregel-Gl2.png)
![= RT{ [ f(x+α)-f(x) ]⁄α + [ g(x+α)-g(x) ]⁄α }](Gleichungen/Beispiel-Summenregel-Gl3.png)
![= RT{ [ f(x+α)-f(x) ]⁄α } + RT{ [ g(x+α)-g(x) ]⁄α }](Gleichungen/Beispiel-Summenregel-Gl4.png)
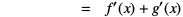 .
.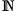 ist differenzierbar. Man erhält für die Steigung zwischen zwei infinitesimal benachbarten Punkten P(x ; xn) und Q(x+α ; (x+α)n)
ist differenzierbar. Man erhält für die Steigung zwischen zwei infinitesimal benachbarten Punkten P(x ; xn) und Q(x+α ; (x+α)n)![m = [(x+α)^n - x^n]⁄[(x+α) - x]](Gleichungen/Beispiel-Potenzregel-Gl1.png)
![= [x^n + n⋅x^(n−1)⋅α + (Summanden mit mindestens α^2) − x^n]⁄[α]](Gleichungen/Beispiel-Potenzregel-Gl2.png)
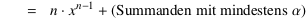 .
.![p_n'(x) = RT[n⋅x^(n-1) + (Summanden mit mindestens α)] = n⋅x^(n-1)](Gleichungen/Beispiel-Potenzregel-Gl4.png) .
.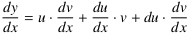 .
.![(u⋅v)'(x) = RT[(dy)⁄(dx)] = (u)⋅RT[(dv)⁄(dx)] + RT[(du)⁄(dx)]⋅(v) + RT[(du)⋅(dv)⁄(dx)]](Gleichungen/Beispiel-Produktregel-Gl2.png)
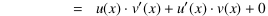 ,
,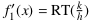 .
.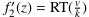 . Gesucht ist
. Gesucht ist 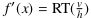 .
. 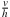 mit dem infinitesimalen k erweitern und erhält
mit dem infinitesimalen k erweitern und erhält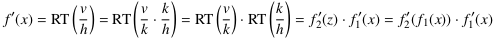 .
.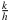 und
und 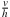 null, was sogar deren reelle Teile sind. Also gilt auch f1'(x) = 0 und f'(x) = 0 und die Ableitung der Verkettung ist in der Form 0 = f'(x) = f2'(f1(x)) ⋅ 0 dieselbe wie im 1. Fall.
null, was sogar deren reelle Teile sind. Also gilt auch f1'(x) = 0 und f'(x) = 0 und die Ableitung der Verkettung ist in der Form 0 = f'(x) = f2'(f1(x)) ⋅ 0 dieselbe wie im 1. Fall.




