Integralrechnung
- Inhalt der Fläche unter dem Graphen der Quadratfunktion mit f(x) = x2 zwischen den Grenzen a = 0 und b = 4
- Zunächst ist die Funktion f hyperreell erweitert zu denken. Das Intervall [0; 4] werde dann in N, das heißt infinit viele Abschnitte der Länge dx unterteilt. N ist eine hypernatürliche Zahl. Es gilt also dx =
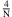 , und es entstehen die Teilungsstellen x i mit x i = i ⋅ dx, wobei i alle (hyper-)natürlichen Zahlen von 1 bis N durchlaufen soll. Es entstehen Rechtecke mit dem Flächeninhalt A i = f(i ⋅ dx) ⋅ dx = (i ⋅ dx)2 ⋅ dx, die man berechnen und aufsummieren kann. Man erhält
, und es entstehen die Teilungsstellen x i mit x i = i ⋅ dx, wobei i alle (hyper-)natürlichen Zahlen von 1 bis N durchlaufen soll. Es entstehen Rechtecke mit dem Flächeninhalt A i = f(i ⋅ dx) ⋅ dx = (i ⋅ dx)2 ⋅ dx, die man berechnen und aufsummieren kann. Man erhält
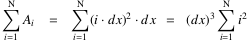 .
.
Für die Summe kann man einen einfacheren Ausdruck zum Beispiel aus einer Formelsammlung gewinnen und schreibt mit dx = 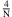
![mit i von 1 bis N: ∑A_i = [4^3 ⁄ N^3] ⋅ [(N^3 ⁄3) + (N^2 ⁄2) + (N⁄6)]](Gleichungen/Beispiel-Parabelflaeche-Gl2.png) ,
,
was ausmultipliziert
![mit i von 1 bis N: ∑A_i = 4^3 ⋅ [1⁄3 + 1⁄(2N) + 1⁄(6N^2)]](Gleichungen/Beispiel-Parabelflaeche-Gl3.png)
ergibt. Die beiden letzten Summanden in der Klammer sind infinitesimal und somit im Reellen unbedeutend. Man erhält als reellen Teil den gesuchten Flächeninhalt unter der Parabel:
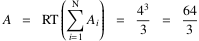 .
.
- Integralfunktion zur Kubikfunktion k mit k(x) = x3
- Der Einfachheit halber liege die untere Grenze bei a = 0, die obere Grenze sei variabel mit der Bezeichnung b. Dann ist zu berechnen
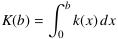 .
.
Das Intervall [0 ; b] werde in infinit viele Abschnitte zerlegt, die hypernatürliche Anzahl sei Ν. Die Länge jedes Intervalls ist dann 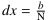 . Die Unterteilungspunkte sind x0 = 0,..., xi = i⋅dx,..., xΝ = b. Somit lässt sich die Fläche zwischen dem Graphen und der x-Achse mit rechteckigen Streifen der Breite dx überdecken, die jeweilige Höhe beträgt k(xi). Damit berechnet sich der Flächeninhalt des i-ten Streifens zu Fi = (i⋅dx)3 ⋅ dx, und für die Summe aller Streifeninhalte erhält man dann
. Die Unterteilungspunkte sind x0 = 0,..., xi = i⋅dx,..., xΝ = b. Somit lässt sich die Fläche zwischen dem Graphen und der x-Achse mit rechteckigen Streifen der Breite dx überdecken, die jeweilige Höhe beträgt k(xi). Damit berechnet sich der Flächeninhalt des i-ten Streifens zu Fi = (i⋅dx)3 ⋅ dx, und für die Summe aller Streifeninhalte erhält man dann
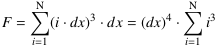 .
.
Die Summe der ersten Ν dritten Potenzen natürlicher Zahlen kann in anderer Form geschrieben werden, was man zum Beispiel in einer Formelsammlung finden kann. Es gilt – auch für hypernatürliche Ν –
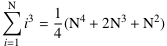 ,
,
also erhält man
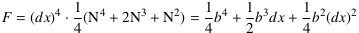 ,
,
wovon der reelle Teil zu bilden ist. Man erhält als Integralfunktion
![K(b) = ∫_0^b k(x)⋅dx = RT[1⁄4 b^4 + 1⁄2 b^3 dx + 1⁄4 b^2 (dx)^2] = 1⁄4 b^4](Gleichungen/Beispiel-Integralfunktion-Gl6.png) .
.
Die Variable b diente nur der Unterscheidung der variablen oberen Grenze von der eigentlichen Variablen x. Die gesuchte Integralfunktion lautet also
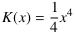 .
.
- Regel für die partielle Integration
- Es gilt die Produktregel der Differentialrechnung, (u⋅v)' = u⋅v' + v⋅u'. In Differentialen ausgedrückt d(u⋅v) = u⋅dv + v⋅du. Die Integration ergibt
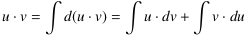
oder, umgestellt,
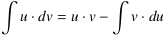 .
.
<nach oben>
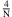 , und es entstehen die Teilungsstellen x i mit x i = i ⋅ dx, wobei i alle (hyper-)natürlichen Zahlen von 1 bis N durchlaufen soll. Es entstehen Rechtecke mit dem Flächeninhalt A i = f(i ⋅ dx) ⋅ dx = (i ⋅ dx)2 ⋅ dx, die man berechnen und aufsummieren kann. Man erhält
, und es entstehen die Teilungsstellen x i mit x i = i ⋅ dx, wobei i alle (hyper-)natürlichen Zahlen von 1 bis N durchlaufen soll. Es entstehen Rechtecke mit dem Flächeninhalt A i = f(i ⋅ dx) ⋅ dx = (i ⋅ dx)2 ⋅ dx, die man berechnen und aufsummieren kann. Man erhält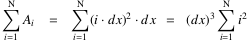 .
.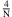
![mit i von 1 bis N: ∑A_i = [4^3 ⁄ N^3] ⋅ [(N^3 ⁄3) + (N^2 ⁄2) + (N⁄6)]](Gleichungen/Beispiel-Parabelflaeche-Gl2.png) ,
,![mit i von 1 bis N: ∑A_i = 4^3 ⋅ [1⁄3 + 1⁄(2N) + 1⁄(6N^2)]](Gleichungen/Beispiel-Parabelflaeche-Gl3.png)
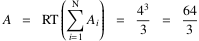 .
.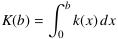 .
.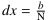 . Die Unterteilungspunkte sind x0 = 0,..., xi = i⋅dx,..., xΝ = b. Somit lässt sich die Fläche zwischen dem Graphen und der x-Achse mit rechteckigen Streifen der Breite dx überdecken, die jeweilige Höhe beträgt k(xi). Damit berechnet sich der Flächeninhalt des i-ten Streifens zu Fi = (i⋅dx)3 ⋅ dx, und für die Summe aller Streifeninhalte erhält man dann
. Die Unterteilungspunkte sind x0 = 0,..., xi = i⋅dx,..., xΝ = b. Somit lässt sich die Fläche zwischen dem Graphen und der x-Achse mit rechteckigen Streifen der Breite dx überdecken, die jeweilige Höhe beträgt k(xi). Damit berechnet sich der Flächeninhalt des i-ten Streifens zu Fi = (i⋅dx)3 ⋅ dx, und für die Summe aller Streifeninhalte erhält man dann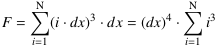 .
.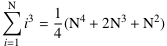 ,
,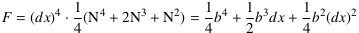 ,
, ![K(b) = ∫_0^b k(x)⋅dx = RT[1⁄4 b^4 + 1⁄2 b^3 dx + 1⁄4 b^2 (dx)^2] = 1⁄4 b^4](Gleichungen/Beispiel-Integralfunktion-Gl6.png) .
.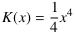 .
.
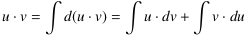
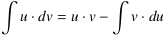 .
.




