Hauptsatz der Differential- und Integralrechnung
- Dieser zentrale Satz der Analysis zeigt, dass Differenzieren und Integrieren gegensätzliche Operationen bei Funktionen sind, und besteht aus zwei Teilen.
- „Differenzieren”: Ist f eine reelle Funktion und Fa eine zugehörige Integralfunktion, dann ist die Ableitung Fa' die Integrandenfunktion.
Denn:
Es sei
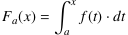
die zu f gehörige Integralfunktion zur unteren Grenze a. Verschiebt man die obere Grenze des Integrals um ein infinitesimales h, dann verändert sich das Integral um
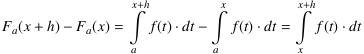 .
.
Es handelt sich also um den Flächeninhalt eines infinitesimalen Streifens der Breite h unter dem Graphen der ins Hyperreelle erweiterten Funktion *f. Da sich alle Funktionswerte wegen deren gleichmäßiger Stetigkeit von *f nur infinitesimal unterscheiden, kann sich dieser Flächeninhalt gegenüber dem Rechtecksinhalt f(x)⋅h höchstens um den Inhalt eines Rechtecks mit Breite h und nicht negativer infinitesimaler Höhe λ unterscheiden.
![[f(x)−λ]⋅h ≤ F_a(x+h)−F_a(x) ≤ [f(x)+λ]⋅h](Gleichungen/Beispiel-Hauptsatz-GlDiff3.png)
Division durch h ergibt je nach Vorzeichen von h
![f(x)−λ ≤ [ F_a(x+h)−F_a(x) ]⁄h ≤ f(x)+λ](Gleichungen/Beispiel-Hauptsatz-GlDiff4.png)
oder
![f(x)−λ ≥ [ F_a(x+h)−F_a(x) ]⁄h ≥ f(x)+λ](Gleichungen/Beispiel-Hauptsatz-GlDiff5.png) .
.
Der Übergang zum reellen Teil ergibt in beiden Fällen
![f(x) ≤ RT{ [ F_a(x+h)−F_a(x) ]⁄h } ≤ f(x)](Gleichungen/Beispiel-Hauptsatz-GlDiff6.png) .
.
Es gilt also tatsächlich Fa' = f
- „Integrieren”: Ist F eine beliebige Stammfunktion von f, dann gilt
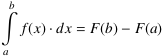 .
.
Denn:
Die Funktion Fa sei eine spezielle Stammfunktion von f. Sie hat die Eigenschaft
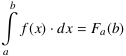
und erfüllt wegen
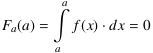
die Behauptung. Weil jede Stammfunktion F genau wie Fa als Ableitung dieselbe Funktion f besitzt, können sich F und Fa nur um eine konstante Funktion C unterscheiden, Fa = F + C, denn nur konstante Funktionen fallen beim Differenzieren fort: C'(x) = 0. Damit hat es auf Differenzen keinen Einfluss. Wegen C(b)−C(a) = 0 gilt dann
F(b)−F(a) = (Fa+C)(b)−(Fa+C)(a) = (Fa(b)+C(b))−(Fa(a)+C(a)) = F(b)−F(a),
also
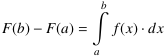 .
.
<nach oben>
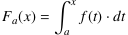
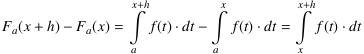 .
.![[f(x)−λ]⋅h ≤ F_a(x+h)−F_a(x) ≤ [f(x)+λ]⋅h](Gleichungen/Beispiel-Hauptsatz-GlDiff3.png)
![f(x)−λ ≤ [ F_a(x+h)−F_a(x) ]⁄h ≤ f(x)+λ](Gleichungen/Beispiel-Hauptsatz-GlDiff4.png)
![f(x)−λ ≥ [ F_a(x+h)−F_a(x) ]⁄h ≥ f(x)+λ](Gleichungen/Beispiel-Hauptsatz-GlDiff5.png) .
.![f(x) ≤ RT{ [ F_a(x+h)−F_a(x) ]⁄h } ≤ f(x)](Gleichungen/Beispiel-Hauptsatz-GlDiff6.png) .
.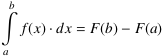 .
.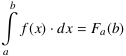
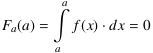
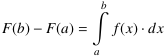 .
.




